题目内容
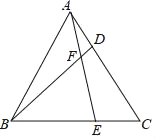
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 为
为![]() 边上的一个动点(与点
边上的一个动点(与点![]() 、
、![]() 不重合),
不重合),![]() ,
,![]() 交对角线
交对角线![]() 于点
于点![]() ,
,![]() 交对角线
交对角线![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
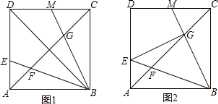
![]() 如图
如图![]() ,联结
,联结![]() ,求证:
,求证:![]() ,并写出
,并写出![]() 的值;
的值;
![]() 联结
联结![]() ,如图
,如图![]() ,若设
,若设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
![]() 当
当![]() 为边
为边![]() 的三等分点时,求
的三等分点时,求![]() 的面积.
的面积.
【答案】![]() 证明见解析;
证明见解析;![]() ;(2)
;(2)![]() ;
;![]() .
.
【解析】
(1)通过正方形性质得![]() ,进而证明
,进而证明![]() ,利用相似三角形性质即可解题,(2)根据相似得
,利用相似三角形性质即可解题,(2)根据相似得![]() ,即
,即![]() ,在直角三角形EGH中勾股定理即可解题,(3)利用三等分点,分类讨论M的位置,求出FG和EH的长即可解题.
,在直角三角形EGH中勾股定理即可解题,(3)利用三等分点,分类讨论M的位置,求出FG和EH的长即可解题.
![]() 证明:∵四边形
证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,又
,又![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 如图
如图![]() ,作
,作![]() 于
于![]() ,
,
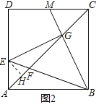
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
![]() 当
当![]() 时,
时,
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,则
,则![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,
时,
![]() ,
,
∴![]() ,
,
∴![]() ,则
,则![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目