题目内容
【题目】如图,已知Rt△ABC中,∠C=90°,AC=8cm,AB=12cm,点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,速度均为1cm/s.以AQ、PQ为边作AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤6).解答下列问题:
(1)当t为何值时,AQPD为矩形.
(2)当t为何值时,AQPD为菱形.
(3)是否存在某一时刻t,使四边形AQPD的面积等于四边形PQCB的面积,若存在,请求出t值,若不存在,请说明理由.

【答案】(1) 当t=![]() 时,AQPD是矩形;(2) 当t=
时,AQPD是矩形;(2) 当t=![]() 时,□AQPD是菱形;(3)
时,□AQPD是菱形;(3) ![]()
【解析】
(1)利用矩形的性质得到△APQ∽△ABC,利用相似三角形对应边的比相等列出比例式即可求得t值;
(2)利用菱形的对角线相互垂直平分解答;
(3)过点P作PM⊥AC于M.先表示出△APQ的面积和S四边形PQCB=S△ABC﹣S△APQ,进而建立方程即可得出结论.
解:(1)如图2,当AQPD是矩形时,PQ⊥AC,
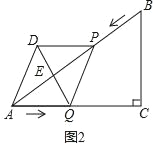
∴PQ∥BC,
∴△APQ∽△ABC
∴![]() =
=![]() ,
,
由运动知,QA=t,BP=t,
∴AP=AB﹣BP=12﹣t,
即,![]() =
=![]() ,
,
解之 t=![]() ,
,
∴当t=![]() 时,AQPD是矩形;
时,AQPD是矩形;
(2)当AQPD是菱形时,DQ⊥AP,AE=![]() AP
AP
则 cos∠BAC=![]() =
=![]() ,
,
由运动知,QA=t,BP=t,
∴AP=AB﹣BP=12﹣t,AE=6﹣![]() t,
t,
∴![]()
解之 t=![]() ,
,
所以当t=![]() 时,□AQPD是菱形;
时,□AQPD是菱形;
(3)存在时间t,使四边形AQPD的面积等于四边形PQCB的面积.
在Rt△ABC中,根据勾股定理得,BC=4![]() ,
,
如图3,过点P作PM⊥AC于M.
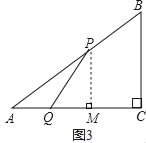
则![]() =
=![]() ,
,
即![]() =
=![]() ,
,
故PM=![]() (12﹣t).
(12﹣t).
∴S△APQ=![]() AQ×PM=
AQ×PM=![]() ×t×
×t×![]() (12﹣t),
(12﹣t),
∴S四边形PQCB=S△ABC﹣S△APQ=![]() ×4
×4![]() ×8﹣
×8﹣![]() ×t×
×t×![]() (12﹣t),
(12﹣t),
∵四边形AQPD的面积等于四边形PQCB的面积,
∴2×![]() ×t×
×t×![]() (12﹣t)=
(12﹣t)=![]() ×4
×4![]() ×8﹣
×8﹣![]() ×t×
×t×![]() (12﹣t),
(12﹣t),
∴t=![]() (舍)或t=
(舍)或t=![]() .
.

 阅读快车系列答案
阅读快车系列答案