Question

【题目】已知：直线，为图形内一点，连接，．

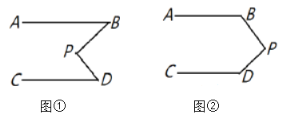
（1）如图①，写出，，之间的等量关系，并证明你的结论；

（2）如图②，请直接写出，，之间的关系式；

（3）你还能就本题作出什么新的猜想？请画图并写出你的结论（不必证明）．

Answer 1

【答案】（1），见解析；（2）；（3），见解析

【解析】

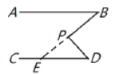
（1）如图①，延长交于点，根据两直线平行，内错角相等可得，再根据三角形外角的性质即可得解；

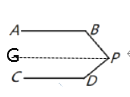
（2）如图②中，过P作PG∥AB，利用平行线的性质即可解决问题；

(3) 如图③,在利用外角的性质以及两直线平行，内错角相等的性质，即可得出．

证明：（1）如图①，延长交于点．

在中则有．

（三角形一个外角等于和它不相邻的两个内角的和）

又，

（两直线平行，内错角相等）

．

．

（图①） （图②）

（2）如图②中，过P作PG∥AB，

∵AB//CD

∴PG//CD

∵AB//PG

∴∠ABP+∠BPG=180°

∵PG//CD

∴∠GPD+∠PDC=180°

∴∠ABP+∠BPG +∠GPD+∠PDC =360°

∴

故答案为：．

（3）如图③．证明如下：

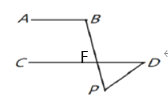
（图③）

在中则有．（三角形一个外角等于和它不相邻的两个内角的和）

又，

（两直线平行，内错角相等）

．