Question

【题目】在一次数学兴趣小组活动中，小明利用同弧所对的圆周角及圆心角的性质探索了一些问题，下面请你和小明一起进入探索之旅．

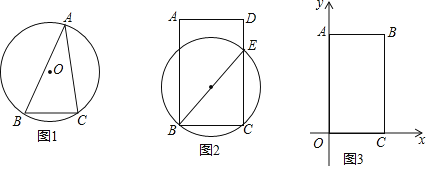
（1）如图1，△ABC中，∠A=30°，BC=2，则△ABC的外接圆的半径为 ；

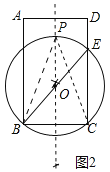
（2）如图2，在矩形ABCD中，请利用以上操作所获得的经验，在矩形ABCD内部用直尺与圆规作出一点P，点P满足；∠BPC=∠BEC，且PB=PC；（要求：用直尺与圆规作出点P，保留作图痕迹．）

（3）如图3，在平面直角坐标系的第一象限内有一点B，坐标为（2，m），过点B作AB⊥y轴，BC⊥x轴，垂足分别为A、C，若点P在线段AB上滑动（点P可以与点A、B重合），发现使得∠OPC=45°的位置有两个，则m的取值范围为 ．

Answer 1

【答案】(1)2；（2）详见解析；（3）2≤m＜1+.

【解析】

（1）连接OB、OC，只要证明△OBC是等边三角形即可．

（2）如图2中，作BC的垂直平分线，交BE于点O，以O为圆心，OB为半径作圆，交垂直平分线于点P，则点P为所求．

（3）如图3中，在x轴上方作△OKC，使得△OKC是以OC为斜边的等腰直角三角形，作KE⊥AB于E．当EK=KC=时，以K为圆心，KC为半径的圆与AB相切，此时m=BC=1+，在AB上只有一个点P满足∠OPC=OKC=45°，当BK=时，在AB上恰好有两个点P满足∠OPC=OKC=45°，此时m=BC=2，由此不难得出结论．

（1）如图1中，连接OB、OC．

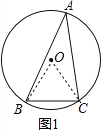
∵∠BOC=2∠A，∠A=30°，

∴∠BOC=60°，

∵OB=OC，

∴△OBC是等边三角形，

∴OB=OC=BC=2；

（2）如图2中，作BC的垂直平分线，交BE于点O；

以O为圆心，OB为半径作圆，交垂直平分线于点P，

则点P为所求．

（3）如图3中，在x轴上方作△OKC，使得△OKC是以OC为斜边的等腰直角三角形，作KE⊥AB于E．

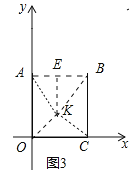
∵OC=2，

∴OK=KC=，

当EK=KC=时，以K为圆心，KC为半径的圆与AB相切，此时m=BC=1+，在AB上只有一个点P满足∠OPC=OKC=45°，

当BK=时，在AB上恰好有两个点P满足∠OPC=OKC=45°，此时m=BC=2，

综上所述，满足条件的m的值的范围为2≤m＜1+．