题目内容
【题目】观察下表： 我们把某格中字母和所得到的多项式称为特征多项式，例如第1格的“特征多项式”为4x+y，回答下列问题：
序号 | 1 | 2 | 3 | … |
图形 | x x | x x x | x x x x | … |
（1）第3格的“特征多项式”为 ， 第4格的“特征多项式”为 ， 第n格的“特征多项式”为；
（2）若第1格的“特征多项式”的值为﹣10，第2格的“特征多项式”的值为﹣16． ①求x，y的值；
②在①的条件下，第n格的“特征多项式”是否有最小值？若有，求出最小值和相应的n值；若没有，请说明理由．
【答案】
（1）16x+9y；25x+16y；（n+1）2x+n2y
（2）解：①∵第1格的“特征多项式”的值为﹣8，第2格的“特征多项式”的值为﹣11，
∴根据题意可得： 
，
解得：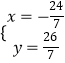 
；
②有最小值，
将x=﹣ 
，y= 
代入（n+1）2x+n2y=（﹣ ）（n+1）2+ n2= 
（n﹣12）2﹣ 
，
当n=12时，最小值为﹣
【解析】解：（1）第3格的“特征多项式”为：16x+9y；第4格的“特征多项式”为：25x+16y； 第n格的“特征多项式”为：（n+1）2x+n2y；
故答案为：16x+9y；25x+16y；（n+1）2x+n2y；
（1）利用已知表格中x，y个数变化规律得出第2格的“特征多项式”以及第n格的“特征多项式”；（2）①利用（1）中所求得出关于x，y的等式组成方程组求出答案；②利用二次函数最值求法得出答案．
练习册系列答案
相关题目
