题目内容
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC= ![]() .
. 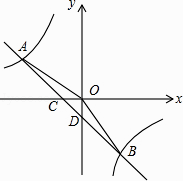
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
【答案】
(1)解:过点A作AE⊥x轴于点E,如图所示.
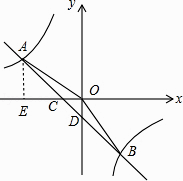
设反比例函数解析式为y= ![]() .
.
∵AE⊥x轴,
∴∠AEO=90°.
在Rt△AEO中,AO=5,sin∠AOC= ![]() ,∠AEO=90°,
,∠AEO=90°,
∴AE=AOsin∠AOC=3,OE= ![]() =4,
=4,
∴点A的坐标为(﹣4,3).
∵点A(﹣4,3)在反比例函数y= ![]() 的图象上,
的图象上,
∴3= ![]() ,解得:k=﹣12.
,解得:k=﹣12.
∴反比例函数解析式为y=﹣ ![]()
(2)解:∵点B(m,﹣4)在反比例函数y=﹣ ![]() 的图象上,
的图象上,
∴﹣4=﹣ ![]() ,解得:m=3,
,解得:m=3,
∴点B的坐标为(3,﹣4).
设直线AB的解析式为y=ax+b,
将点A(﹣4,3)、点B(3,﹣4)代入y=ax+b中得:
![]() ,解得:
,解得: ![]() ,
,
∴一次函数解析式为y=﹣x﹣1.
令一次函数y=﹣x﹣1中y=0,则0=﹣x﹣1,
解得:x=﹣1,即点C的坐标为(﹣1,0).
S△AOB= ![]() OC(yA﹣yB)=
OC(yA﹣yB)= ![]() ×1×[3﹣(﹣4)]=
×1×[3﹣(﹣4)]= ![]()
【解析】(1)过点A作AE⊥x轴于点E,设反比例函数解析式为y= ![]() .通过解直角三角形求出线段AE、OE的长度,即求出点A的坐标,再由点A的坐标利用待定系数法求出反比例函数解析式即可;(2)由点B在反比例函数图象上可求出点B的坐标,设直线AB的解析式为y=ax+b,由点A、B的坐标利用待定系数法求出直线AB的解析式,令该解析式中y=0即可求出点C的坐标,再利用三角形的面积公式即可得出结论.
.通过解直角三角形求出线段AE、OE的长度,即求出点A的坐标,再由点A的坐标利用待定系数法求出反比例函数解析式即可;(2)由点B在反比例函数图象上可求出点B的坐标,设直线AB的解析式为y=ax+b,由点A、B的坐标利用待定系数法求出直线AB的解析式,令该解析式中y=0即可求出点C的坐标,再利用三角形的面积公式即可得出结论.

【题目】三五三七鞋厂为了了解初中学生穿鞋的鞋号情况,对红华中学初二(1)班的20名男生所穿鞋号统计如下表:
鞋号 | 23.5 | 24 | 24.5 | 25 | 25.5 | 26 |
人数 | 3 | 4 | 4 | 7 | 1 | 1 |
(1)写出男生鞋号数据的平均数,中位数,众数;
(2)在平均数,中位数和众数中,鞋厂最感兴趣的是什么?
【题目】观察下表: 我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
序号 | 1 | 2 | 3 | … |
图形 | x x | x x x | x x x x | … |
(1)第3格的“特征多项式”为 , 第4格的“特征多项式”为 , 第n格的“特征多项式”为;
(2)若第1格的“特征多项式”的值为﹣10,第2格的“特征多项式”的值为﹣16. ①求x,y的值;
②在①的条件下,第n格的“特征多项式”是否有最小值?若有,求出最小值和相应的n值;若没有,请说明理由.