题目内容
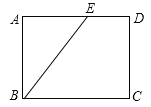
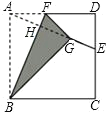
【题目】如图,正方形纸片ABCD的边长为12,E是边CD的中点,连接AE,折叠该纸片,使点A落在AE上的G点,并使折痕经过点B,得到折痕BF,点F在AD上,若DE=5,则GE的长为__________.

【答案】![]()
【解析】
由折叠及轴对称的性质可知,△ABF≌△GBF,BF垂直平分AG,先证△ABF≌△DAE,推出AF的长,再利用勾股定理求出BF的长,最后在Rt△ADF中利用面积法可求出AH的长,可进一步求出AG的长,GE的长.
∵四边形ABCD为正方形,
∴AB=AD=12,∠BAD=∠D=90°,
由折叠及轴对称的性质可知,△ABF≌△GBF,BF垂直平分AG,
∴BF⊥AE,AH=GH,
∴∠BAH+∠ABH=90°,
又∵∠FAH+∠BAH=90°,
∴∠ABH=∠FAH,
∴△ABF≌△DAE(ASA),
∴AF=DE=5,
在Rt△ABF中,
BF=![]() =13,
=13,
S△ABF=![]() ABAF=
ABAF=![]() BFAH,
BFAH,
∴12×5=13AH,
∴AH=![]() ,
,
∴AG=2AH=![]() ,
,
∵AE=BF=13,
∴GE=AE-AG=13-![]() =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目