题目内容
【题目】某数学兴趣小组想测量河流的宽度AB,河流两岸AC,BD互相平行,河流对岸有两棵树A和C,且A、C之间的距离是60m,他们在D处测得∠BDC=36°,前行140米后测得∠BPA=45°,请根据这些数据求出河流的宽度.
(结果精确到0.1米,参考数据:tan36°≈0.73,sin36°≈0.59,cos36°≈0.81)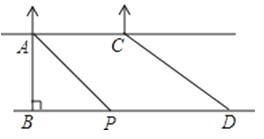
【答案】解:作CH⊥BD,则BH=AC=60米,设AB为x米,则CH为x米,
在Rt△ABP中,tan45°=1,
∴BP=x,
∴HD=BP+PD﹣BH=x+140﹣60=(x+80)米,
在Rt△CHD中,
∵tan∠CDH= ![]() ,
,
∴x+80=![]() ,
,
∴x=(x+80)tan36°,
∴x≈216.3(米),
答:河流的宽度约为216.3米.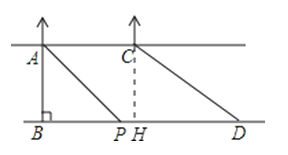
【解析】作CH⊥BD,设AB为x米,则CD为x米,在Rt△ABP中,易求HD,在Rt△CHD中,根据36度角的锐角三角函数可建立方程,解方程求出x的值即可.

练习册系列答案
相关题目
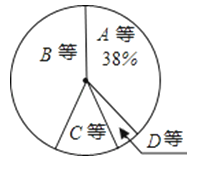
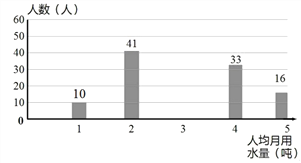
【题目】某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
等级 | 成绩x/分 | 频数/(人数) | 频率 |
A | 9.0≤x≤10.0 | a | m |
B | 7.0≤x<9.0 | 23 | 0.46 |
C | 6.0≤x<7.0 | b | n |
D | 0.0≤x<6.0 | 3 | 0.06 |
合计 | 50 | 1.00 |
(1)在被调查的男生中,成绩为B等级的有多少人,占被调查男生人数的多少,m 等于 多少;
(2)求a,b,n的值;
(3)如果该校七年级共有200名男生,试估计这200名男生中成绩达到A等级和B等级的共有多少人.