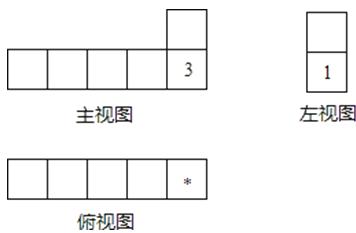
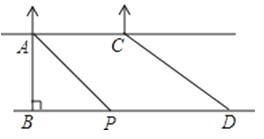
题目内容
【题目】我国是世界上严重缺水的国家之一,某校为了组织“节约用水从我做起”活动,随机调查了本校120名同学家庭月人均用水量和节水措施情况,如图1、图2是根据调查结果做出的统计图的一部分.请根据信息解答下列问题:
(1)图1中淘米水浇花所在的扇形的圆心角度数为__________________;
(2)补全图2;
(3)求120名同学家庭月人均用水量的中位数和众数;
(4)如果全校学生家庭总人数为3000人,根据这120名同学家庭月人均用水量,估计全校学生家庭月用水总量是多少吨?

图1
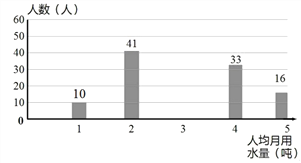
图2
【答案】54°
【解析】分析:(1)根据单位1,减去其着的百分比求出淘米水浇花的百分比,乘以390即可得到结果;
(4)由总人数减去其它4组的人数求出人均用水量为3吨的人数,补全统计图即可;
(3)将人均用水量按照从小到大顺序排列,找出第90,91个数字,求出平均值即可得到中位数.出现次数最多的数是众数;
(4)如果全校学生家庭总人数为3000人,根据这120名同学家庭月人均用水量,估计全校学生家庭月用水总量是多少吨.
详解:(1)图1中淘米水浇花所在的扇形的圆心角度数为360°×(1-11%-44%-30%)=54°;
(2)人均用水量为3吨的人数为120-(10+41+33+16)=20(人),
补全图如图所示;
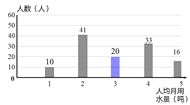
(3)观察条形统计图,从小到大排列后,第60,61个数为3,3,众数为2,
则这120名同学家庭月人均用水量的中位数是3吨, 众数为2.
(4)(30×1+41×2+20×3+33×4+16×5)÷120=3.2,
3.2×3000=9600(吨),
答:全校学生家庭月用水总量是9600吨.

【题目】东门天虹商场购进一批“童乐”牌玩具,每件成本价30元,每件玩具销售单价x(元)与每天的销售量y(件)的关系如下表:
x(元) | … | 35 | 40 | 45 | 50 | … |
y(件) | … | 750 | 700 | 650 | 600 | … |
若每天的销售量y(件)是销售单价x(元)的一次函数
(1)求y与x的函数关系式;
(2)设东门天虹商场销售“童乐”牌儿童玩具每天获得的利润为w(元),当销售单价x为何值时,每天可获得最大利润?此时最大利润是多少?
(3)若东门天虹商场销售“童乐”牌玩具每天获得的利润最多不超过15000元,最低不低于12000元,那么商场该如何确定“童乐”牌玩具的销售单价的波动范围?请你直接给出销售单价x的范围.