ΧβΡΩΡΎ»ί
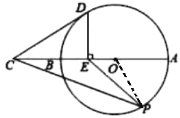
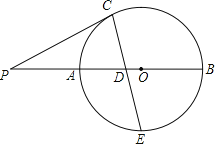
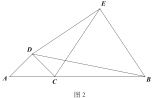
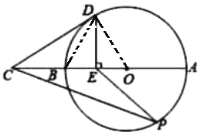
ΓΨΧβΡΩΓΩΙ≈œΘάΑ ΐ―ßΦ“±œ¥οΗγά≠ΥΙ»œΈΣΘΚΓΑ“Μ«–ΤΫΟφΆΦ–Έ÷–ΉνΟάΒΡ «‘≤Γ±Θ°«κ―–ΨΩ»γœ¬ΟάάωΒΡ‘≤Θ°»γΆΦΘ§œΏΕΈAB «Γ―OΒΡ÷±ΨΕΘ§―”≥ΛAB÷ΝΒψCΘ§ ΙBCΘΫOBΘ§ΒψE «œΏΕΈOBΒΡ÷–ΒψΘ§DEΓΆABΫΜΓ―O”ΎΒψDΘ§ΒψP «Γ―O…œ“ΜΕ·ΒψΘ®≤Μ”κΒψAΘ§B÷ΊΚœΘ©Θ§Ν§Ϋ”CDΘ§PEΘ§PCΘ°
Θ®1Θ©«σ÷ΛΘΚCD «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©–ΓΟς‘Ύ―–ΨΩΒΡΙΐ≥Χ÷–ΖΔœ÷![]() «“ΜΗω»ΖΕ®ΒΡ÷ΒΘ°ΜΊ¥π’βΗω»ΖΕ®ΒΡ÷Β «Εύ…ΌΘΩ≤ΔΕ‘–ΓΟςΖΔœ÷ΒΡΫα¬έΦ”“‘÷ΛΟςΘ°
«“ΜΗω»ΖΕ®ΒΡ÷ΒΘ°ΜΊ¥π’βΗω»ΖΕ®ΒΡ÷Β «Εύ…ΌΘΩ≤ΔΕ‘–ΓΟςΖΔœ÷ΒΡΫα¬έΦ”“‘÷ΛΟςΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘΜΘ®2Θ©![]() Θ§ΫβΈω
Θ§ΫβΈω
ΓΨΫβΈωΓΩ
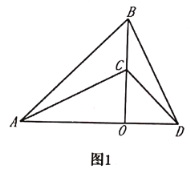
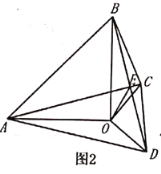
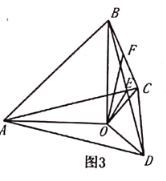
±ΨΧβΩΦ≤ιΝΥ«–œΏΒΡ≈–Ε®”κ–‘÷ ΦΑœύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®”κ–‘÷ Θ°Θ®1Θ©Ν§Ϋ”ODΘ§DBΘ§”…“―÷ΣΩ…ΒΟDE¥Ι÷±ΤΫΖ÷OBΘ§”Ύ «DBΘΫDOΘ§ΕχOBΘΫODΘ§Υυ“‘DBΘΫDOΘΫOBΘ§Φ¥ΓςODB «Β»±Ώ»ΐΫ«–ΈΘ§”Ύ «ΓœBDOΘΫ60ΓψΘ§‘Ό”…Β»―ϋ»ΐΫ«–ΈΒΡ–‘÷ ΦΑ»ΐΫ«–ΈΒΡΆβΫ«–‘÷ Ω…ΒΟΓœCDBΘΫ30ΓψΘ§¥”ΕχΩ…ΒΟΓœODCΘΫ90ΓψΘ§Υυ“‘ODΓΆCDΘ§Υυ“‘CD «Γ―OΒΡ«–œΏΘΜΘ®2Θ©Ν§Ϋ”OPΘ§”…“―÷ΣΧθΦΰΒΟOPΘΫOBΘΫBCΘΫ2OEΘ§‘Όάϊ”ΟΓΑΝΫΉι±Ώ≥…±»άΐΘ§Φ–Ϋ«œύȖ÷ΛΟςΓςOEPΓΉΓςOPCΘ§ΉνΚσ”…œύΥΤ»ΐΫ«–ΈΒΡΕ‘”Π±Ώ≥…±»άΐΒΟΒΫΫα¬έΘ°
ΫβΘΚΘ®1Θ©»γ¥πΆΦΘ§Ν§Ϋ”ODΘ§DBΘ§ΓΏΒψE «œΏΕΈOBΒΡ÷–ΒψΘ§DEΓΆABΫΜΓ―O”ΎΒψDΘ§ΓύDE¥Ι÷±ΤΫΖ÷OBΘ§ΓύDBΘΫDOΘ°ΓΏDOΘΫOBΘ§ΓύDBΘΫDOΘΫOBΘ§ΓύΓςODB «Β»±Ώ»ΐΫ«–ΈΘ§ΓύΓœBDOΘΫΓœDBOΘΫ60ΓψΘ°ΓΏBCΘΫOBΘΫBDΘ§«“ΓœDBEΈΣΓςBDCΒΡΆβΫ«Θ§ΓύΓœBCDΘΫΓœBDCΘΫ![]() ΓœDBOΘ°ΓΏΓœDBOΘΫ60ΓψΘ§ΓύΓœCDBΘΫ30ΓψΘ°ΓύΓœODCΘΫΓœBDOΘΪΓœBDCΘΫ60ΓψΘΪ30ΓψΘΫ90ΓψΘ§ΓύODΓΆCDΘ§ΓύCD «Γ―OΒΡ«–œΏΘΜ
ΓœDBOΘ°ΓΏΓœDBOΘΫ60ΓψΘ§ΓύΓœCDBΘΫ30ΓψΘ°ΓύΓœODCΘΫΓœBDOΘΪΓœBDCΘΫ60ΓψΘΪ30ΓψΘΫ90ΓψΘ§ΓύODΓΆCDΘ§ΓύCD «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©’βΗω»ΖΕ®ΒΡ÷Β «![]() Θ°
Θ°
÷ΛΟςΘΚ»γ¥πΆΦΘ§Ν§Ϋ”OPΘ§ΓΏOPΘΫOBΘΫBCΘΫ2OEΘ§Γύ![]() ΘΫ
ΘΫ![]() ΘΫ
ΘΫ![]() Θ§”÷ΓΏΓœCOPΘΫΓœPOEΘ§ΓύΓςOEPΓΉΓςOPCΘ§Γύ
Θ§”÷ΓΏΓœCOPΘΫΓœPOEΘ§ΓύΓςOEPΓΉΓςOPCΘ§Γύ![]() ΘΫ
ΘΫ![]() ΘΫ
ΘΫ![]() Θ°
Θ°