题目内容
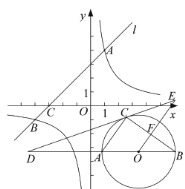
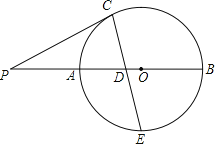
【题目】如图,AB为⊙O的直径,P为BA延长线上一点,点C在⊙O上,连接PC,D为半径OA上一点,PD=PC,连接CD并延长交⊙O于点E,且E是![]() 的中点.
的中点.
(1)求证:PC是⊙O的切线;
(2)求证:CDDE=2ODPD;
(3)若AB=8,CDDE=15,求PA的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接OC,OE,根据等腰三角形的性质得到∠E=∠OCE,求得∠E+∠ODE=90°,得到∠PCD=∠ODE,得到OC⊥PC,于是得到结论;
(2)连接AC,BE,BC,根据相似三角形的性质得到![]() ,推出CDDE=AO2﹣OD2;由△ACP∽△CBP,得到
,推出CDDE=AO2﹣OD2;由△ACP∽△CBP,得到![]() =
=![]() ,
,
得到PD2=PD2+2PDOD+OD2﹣OA2,于是得到结论;
(3)由(2)知,CDDE=AO2﹣OD2;把已知条件代入得到OD=1(负值舍去),求得AD=3,由(2)知,CDDE=2ODPD,于是得到结论.
(1)证明:连接OC,OE,
∵OC=OE,
∴∠E=∠OCE,
∵E是![]() 的中点,
的中点,
∴![]() =
=![]() ,
,
∴∠AOE=∠BOE=90°,
∴∠E+∠ODE=90°,
∵PC=PD,
∴∠PCD=∠PDC,
∵∠PDC=∠ODE,
∴∠PCD=∠ODE,
∴∠PCD+∠OCD=∠ODE+∠E=90°,
∴OC⊥PC,
∴PC是⊙O的切线;
(2)证明:连接AC,BE,BC,
∵∠ACD=∠DBE,∠CAD=∠DEB,
∴△ACD∽△EBD,
∴![]() ,
,
∴CDDE=ADBD=(AO﹣OD)(AO+OD)=AO2﹣OD2;
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠PCO=90°,
∴∠ACP+∠ACO=∠ACO+∠BCO=90°,
∴∠ACP=∠BCO,
∵∠BCO=∠CBO,
∴∠ACP=∠PBC,
∵∠P=∠P,
∴△ACP∽△CBP,
∴![]() =
=![]()
∴PC2=PBPA=(PD+DB)(PD﹣AD)=(PD+OD+OA)(PD+OD﹣OA)=(PD+OD)2﹣OA2=PD2+2PDOD+OD2﹣OA2,
∵PC=PD,
∴PD2=PD2+2PDOD+OD2﹣OA2,
∴OA2﹣OD2=2ODPD,
<>∴CDDE=2ODPD;(3)解:∵AB=8,
∴OA=4,
由(2)知,CDDE=AO2﹣OD2;
∵CDDE=15,
∴15=42﹣OD2,
∴OD=1(负值舍去),
∴AD=3,
由(2)知,CDDE=2ODPD,
∴PD=![]() =
=![]() ,
,
∴PA=PD﹣AD=![]() .
.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案