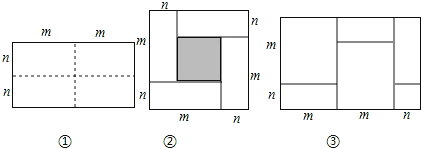
��Ŀ����
����Ŀ����֪��A��D��ֱ��l��ͬ�࣮
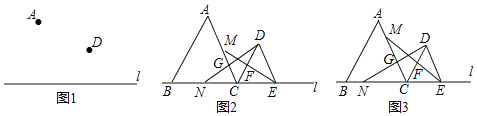
��1����ͼ1����ֱ��l����һ��C��ʹ���߶�AC+DC��С����ͨ����ͼָ����C��λ�ã���
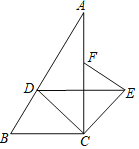
��2����ͼ2����ֱ��l��ȡ����B��E��ǡ����ʹ��ABC����DCE��Ϊ�ȱ������Σ�M��N�ֱ����߶�AC��BC�ϵĶ��㣬����DN��AC�ڵ�G������EM��CD�ڵ�F��
�ٵ���M��N�ֱ���AC��BC���е�ʱ���ж��߶�EM��DN��������ϵ����˵�����ɣ�
����ͼ3������M��N�ֱ�ӵ�A��B��ʼ��AC��BC����ͬ���ٶ����C�����˶�����M��N���C�غ�ʱ�˶�ֹͣ���ж����˶��������߶�GF��ֱ��1��λ�ù�ϵ����˵�����ɣ�
���𰸡���1����������2����EM=DN��FG��l
��������
��1����������A����ֱ��l�ĶԳƵ�A'����DA'��ֱ��l�ڵ�C��
��2�������жϳ�CM=CN����DCN=��ECM=120���������жϳ���CDN�ա�CEM�����ɵó����ۣ�
��ͬ�ٵķ����жϳ���CDN�ա�CEM���ó���CDN=��CEM�������жϳ���DCG�ա�ECF���ó�CF=CG���ó���CFG�ǵȱ������μ��ɵó����ۣ�
��1����ͼ1��ʾ����C������������

��2����EM=DN�����ɣ�
�ߵ�M��N�ֱ���AC��BC���е㣬
��CM=![]() AC��CN=
AC��CN=![]() BC��
BC��
�ߡ�ABC�ǵȱ������Σ�
���ACB=60����AC=BC��
���ECM=120����CM=CN��
���CDE�ǵȱ������Σ�
���DCE=60����CE=CD�����NCD=120����
����CDN����CEM��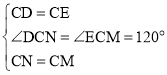 ��
��
���CDN�ա�CEM��
��EM=DN��
��FG��l�����ɣ���ͼ3������FG��

���˶�֪��AM=BN��
��AC=BC��
��CM=BN��
����CDN����CEM��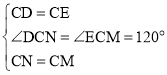 ��
��
���CDN�ա�CEM��
���CDN=��CEM��
�ߡ�ACB=��DCE=60����
���ACD=60��=��DCE��
����DCG����ECF�� ��
��
���DCG�ա�ECF��
��CF=CG��
�ߡ�FCG=60����
���CFG�ǵȱ������Σ�
���CFG=60��=��ECF��
��FG��BC��
����FG��l��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�