Question

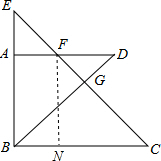
如图所示，在梯形ABCF中，∠ABC=90°，AF∥BC，BA与CF的延长线交于点E，D为AF延长线上一点，且BD⊥CE于G，CF=BC
（1）求证：EF=FD；
（2）若FG=2，CG=6，求四边形ABGF的面积．

Answer 1

（1）证明：过F作FN⊥BC于N，
∵∠ABC=90°，
∴AB∥FN，
∵AD∥BC，
∴四边形AFNB是平行四边形，
AF=BN，AB=FN，
∵FN⊥BC，BD⊥CE，
∴∠FNC=∠BGC=90°，
∵在△BGC和△FNC中

∠C=∠C ∠BGC=∠FNC BC=CF

，
∴△BGC≌△FN（AAS），
∴BG=FN=AB，CG=CN，
∵BC=CF，
∴BN=FG=AF，
∵AD∥BC，∠ABC=90°，BD⊥CF，
∴∠EAF=∠ABC=90°=∠DGF，
∵在△EAF和△DGF中

∠EAF=∠DGF AF=FG ∠EFA=∠DFG

，
∴△EAF≌△DGF（ASA），
∴EF=FD．

（2）由（1）知：CG=CN=6，△EAF≌△DGF，
∴AF=FG=2，
在Rt△FNC中，CF=CG+FG=2+6=8，CN=6，由勾股定理得：FN=

FC2-NC2

=2

7

，
∵由（1）知：AB=FN=2

7

=BG，连接BF，
∴四边形ABGF的面积是：S_△BAF+S_△BGF=

1

2

×AF×AB+

1

2

×BG×FG=

1

2

×2

7

×2+

1

2

×2

7

×2=4

7

，
答：四边形ABGF的面积是4

7

．