题目内容
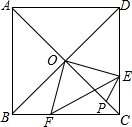
如图，已知四边形ABCD是正方形，分别过A、C两点作l1∥l2，作BM⊥l1于M，DN⊥l1于N，直线MB、ND分别交l2于Q、P．求证：四边形PQMN是正方形．
证明：l1∥l2，BM⊥l1，DN⊥l2，
∴∠QMN=∠P=∠N=90°，
∴四边形PQMN为矩形，
∵AB=AD，∠M=∠N=90°
∠ADN+∠NAD=90°，∠NAD+∠BAM=90°，
∴∠ADN=∠BAM，
又∵AD=BA，
∴Rt△ABM≌Rt△DAN（HL），
∴AM=DN
同理AN=DP，
∴AM+AN=DN+DP，即MN=PN．
∴四边形PQMN是正方形．
∴∠QMN=∠P=∠N=90°，
∴四边形PQMN为矩形，
∵AB=AD，∠M=∠N=90°
∠ADN+∠NAD=90°，∠NAD+∠BAM=90°，
∴∠ADN=∠BAM，
又∵AD=BA，
∴Rt△ABM≌Rt△DAN（HL），
∴AM=DN
同理AN=DP，
∴AM+AN=DN+DP，即MN=PN．
∴四边形PQMN是正方形．
练习册系列答案
阅读快车系列答案
相关题目
