题目内容
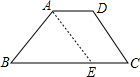
如图等腰梯形ABCD中,AD∥BC,AB=CD,梯形的腰长为6,且BC-AD=6
,则∠B的度数为( )

| 2 |
| A.30° | B.45° | C.60° | D.不确定 |

过点A作AE∥CD交BC于点E,
∵AD∥BC,AB=CD,
∴四边形AECD是平行四边形,AB=CD,
∴AE=CD,CE=AD,
∴AE=AB=6,
∵BE=BC-CE=BC-AD=6
,
∴AB2+AE2=72,BE2=72,
∴AB2+AE2=BE2,
∴∠BAE=90°,
∴∠B=45°.
故选B.
∵AD∥BC,AB=CD,
∴四边形AECD是平行四边形,AB=CD,
∴AE=CD,CE=AD,
∴AE=AB=6,
∵BE=BC-CE=BC-AD=6
| 2 |
∴AB2+AE2=72,BE2=72,
∴AB2+AE2=BE2,
∴∠BAE=90°,
∴∠B=45°.
故选B.


练习册系列答案
相关题目






