题目内容
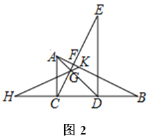
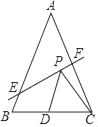
【题目】如图，△ABC的面积是12，AB=AC，BC=3，边AC的垂直平分线交AC于F，交AB于E．点D是BC的中点，点P是EF上的一个动点，则△PCD的周长最小值是( )
A.4B.8C.7D.9.5
【答案】D
【解析】
连接AD，由等腰三角形的性质可得AD⊥BC，CD=1．5，根据三角形的面积公式可求得AD=8，再根据EF是线段AC的垂直平分线，可知点C关于直线EF的对称点为点A，从而可得AD的长为CP+PD的最小值，继而根据三角形周长公式进行求解即可得．
连接AD，
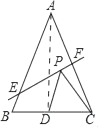
∵△ABC中，AB=AC，点D是BC边的中点，BC=3，
∴AD⊥BC，CD=
BC=1.5，
∴S△ABC=BCAD=×3×AD=12，
解得AD=8，
∵EF是线段AC的垂直平分线，
∴点C关于直线EF的对称点为点A，
∴AD的长为CP+PD的最小值，
∴△CDP的周长最短=CP+PD+CD=AD+CD=8+1.5=9.5，
故选D．
期末金牌卷系列答案
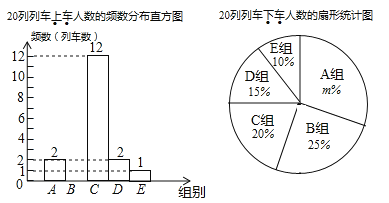
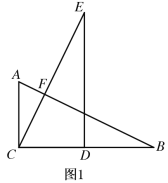
轻松课堂标准练系列答案
【题目】根据重庆轨道集团提供的日客运量统计，2019年2月21日重庆轨道交通首次日客运量突破300万乘次，其中近期开通的重庆轨道交通环线日客运量为21.5万乘次．据了解，某工作日上午7点至9点轨道环线四公里站有20列列车进出站，每列车进出站时，将上车和下车的人数记录下来，各得到20个数据，并将数据进行整理，绘制成了如下两幅不完整统计图．(数据分组为：
组：
，
组：
，
组：
，
组：
，
组：
)
I．上车人数在组的是：190，190，191，192，193，193，195，196，198，198，198，198；
II．上车人数的平均数、中位数如下表：
平均数 | 中位数 | |
上车人数(人) | 194 | a |
根据以上信息，回答下列问题：
(1)请补全频数分布直方图；
(2)表中
________，扇形统计图中
_________，扇形统计图中组所在的圆心角度数为________度；
(3)请利用平均数，估算一周内5个工作日的上午7点至9点重庆轨道环线四公里站的上车总人数．
