题目内容
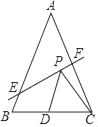
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为边
为边![]() 上的中线,点
上的中线,点![]() 在
在![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() .
.
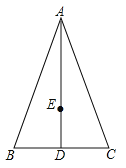
(1)依题意补全图形;
(2)求证:![]() ;
;
(3)若![]() 平分
平分![]() ,则
,则![]() 与
与![]() 满足的等量关系为 .
满足的等量关系为 .
【答案】(1)见详解;(2)证明见详解;(3)∠BAE+∠ABE=60°.
【解析】
(1)根据相关作图技巧,依题意补全图形即可;
(2)由等腰三角形的性质得出∠ABE=∠AFG,∠EAB=∠GAF,证明△EAB≌△GAF(ASA),得出BE=FG,证明△EAB≌△EAC(SAS),得出BE=CE,即可得出结论;
(3)由(2)得∠CAE=∠BAE,△EAB≌△GAF,△EAB≌△EAC,由全等三角形的性质得出AE=AG,∠ABE=∠ACE,由等腰三角形的性质得出∠AEG=∠AGE,证出∠AEG=∠EAG=∠AGE,得出△AGE是等边三角形,由等边三角形的性质得出∠AEG=60°,由三角形的外角性质即可得出结论.
解:(1)依题意补全图形,如图所示:
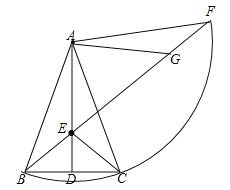
(2)证明:由题意得:AB=AC=AF,
∴∠ABE=∠AFG,
∵∠EAC+∠CAG=∠EAG,∠CAG+∠GAF=∠CAF,∠EAG=∠CAF,
∴∠EAC=∠GAF,
∵AB=AC,AD为边BC上的中线,
∴∠EAC=∠EAB,
∴∠EAB=∠GAF,
在△EAB和△GAF中,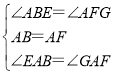 ,
,
∴△EAB≌△GAF(ASA),
∴BE=FG,
在△EAB和△EAC中,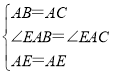 ,
,
∴△EAB≌△EAC(SAS),
∴BE=CE,
∴FG=CE.
(3)由(2)得:∠CAE=∠BAE,△EAB≌△GAF,△EAB≌△EAC,
∴AE=AG,∠ABE=∠ACE,
∴∠AEG=∠AGE,
∵EF平分∠AEC,
∴∠AEG=∠CEG,
∴∠AGE=∠CEG,
∴AG∥CE,
∴∠GAC=∠ACE,
∴∠ABE=∠GAC,
∵∠AEG=∠ABE+∠BAE,∠EAG=∠EAC+∠GAC,
∴∠AEG=∠EAG=∠AGE,
∴△AGE是等边三角形,
∴∠AEG=60°,
∴∠BAE+∠ABE=60°.
故答案为:∠BAE+∠ABE=60°.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案