题目内容
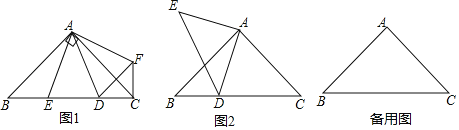
【题目】如图,Rt△ABC≌Rt△CED(∠ACB=∠CDE=90°),点D在BC上,AB与CE相交于点F
(1) 如图1,直接写出AB与CE的位置关系
(2) 如图2,连接AD交CE于点G,在BC的延长线上截取CH=DB,射线HG交AB于K,求证:HK=BK
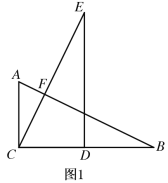
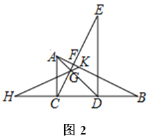
【答案】(1)AB⊥CE;(2)见解析.
【解析】
(1)由全等可得∠ECD=∠A,再由∠B+∠A=90°,可得∠B+ECD=90°,则AB⊥CE.
(2)延长HK于DE交于H,易得△ACD为等腰直角三角形,∠ADC=45°,易得DH=DE,然后证明△DGH≌△DGE,所以∠H=∠E,则∠H=∠B,可得HK=BK.
解:(1)∵Rt△ABC≌Rt△CED,
∴∠ECD=∠A,∠B=∠E,BC=DE,AC=CD
∵∠B+∠A=90°
∴∠B+ECD=90°
∴∠BFC=90°,∴AB⊥CE
(2)在Rt△ACD中,AC=CD,∴∠ADC=45°,
又∵∠CDE=90°,∴∠HDG=∠CDG=45°
∵CH=DB,∴CH+CD=DB+CD,即HD=BC,
∴DH=DE,
在△DGH和△DGE中,
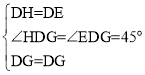
∴△DGH≌△DGE(SAS)
∴∠H=∠E
又∵∠B=∠E
∴∠H=∠B,
∴HK=BK

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目