题目内容
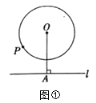
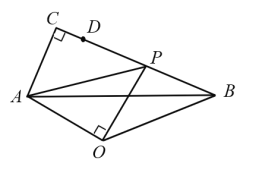
【题目】如图,已知![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 关于
关于![]() 的对称点
的对称点![]() 恰好落在
恰好落在![]() 上.
上.
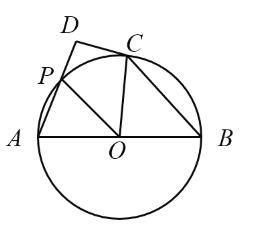
(1)求证:![]() ;
;
(2)过点![]() 作
作![]() 的切线
的切线![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .如果
.如果![]() ,求
,求![]() 的直径.
的直径.
【答案】(1)见解析;(2)4
【解析】
(1)由题意可知![]() ,根据同弧所对的圆心角相等得到
,根据同弧所对的圆心角相等得到![]() ,再根据同弧所对的圆心角和圆周角的关系得出
,再根据同弧所对的圆心角和圆周角的关系得出![]() ,利用同位角相等两直线平行,可得出PO与BC平行;
,利用同位角相等两直线平行,可得出PO与BC平行;
(2)利用切线的性质得到OC垂直于CD,从而得到OC∥AD,即可得到∠APO=∠COP,进一步得出∠APO=∠AOP,确定出![]() 为等边三角形,点
为等边三角形,点![]() ,点
,点![]() 关于
关于![]() 对称,继而得出
对称,继而得出![]() 为等边三角形,可求出∠PCD为30°,在直角三角形PCD中,利用30°所对的直角边等于斜边的一半可得出PD为PC的一半,可得出PD为AB的四分之一,即AB=4PD=4.
为等边三角形,可求出∠PCD为30°,在直角三角形PCD中,利用30°所对的直角边等于斜边的一半可得出PD为PC的一半,可得出PD为AB的四分之一,即AB=4PD=4.
解:(1)证明:∵点![]() 关于
关于![]() 的对称点
的对称点![]() 恰好落在
恰好落在![]() 上.
上.
∴![]() ∴
∴![]() ,∴
,∴![]()
又∵![]() ∴
∴![]() ,
,
∴![]() ;
;
(2)解:连接![]() ,
,
∵![]() 为圆
为圆![]() 的切线,∴
的切线,∴![]() ,又
,又![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ∵
∵![]() .
.
∴![]() 为等边三角形,
为等边三角形,![]() ,
,
又∵点![]() ,点
,点![]() 关于
关于![]() 对称
对称
∴![]() 也为等边三角形,
也为等边三角形,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
在![]() 中
中![]() ,
,
又![]() ,
,
∴![]() .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目