题目内容
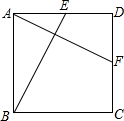
如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG=
,求EB的长.

(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG=
| 2 |

(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD
∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,
在△GAD和△EAB中
,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)EB⊥GD.
理由如下:∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,
∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°-(∠HDM+∠DMH)=180°-90°=90°,
∴EB⊥GD.

(3)连接AC、BD,BD与AC交于点O,
∵AB=AD=2,在Rt△ABD中,DB=
=2
,
在Rt△AOB中,OA=OB,AB=2,由勾股定理得:2AO2=22,
OA=
,
即OG=OA+AG=
+
=2
,
∴EB=GD=
=
=
.


∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,
在△GAD和△EAB中
|
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)EB⊥GD.
理由如下:∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,
∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°-(∠HDM+∠DMH)=180°-90°=90°,
∴EB⊥GD.

(3)连接AC、BD,BD与AC交于点O,
∵AB=AD=2,在Rt△ABD中,DB=
| AB2+AD2 |
| 2 |
在Rt△AOB中,OA=OB,AB=2,由勾股定理得:2AO2=22,
OA=
| 2 |
即OG=OA+AG=
| 2 |
| 2 |
| 2 |
∴EB=GD=
| OG2+OD2 |
| 8+2 |
| 10 |



练习册系列答案
相关题目