题目内容
【题目】如图,正方形ABCD中,E、F均为中点,则下列结论中:①AF⊥DE;②AD=BP;③PE+PF= ![]() PC;④PE+PF=PC.其中正确的是 .
PC;④PE+PF=PC.其中正确的是 . 
【答案】①②③
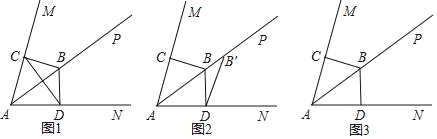
【解析】解:如图1,
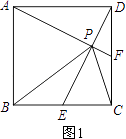
∵正方形ABCD,E,F均为中点,
∴AD=DC=BC,∠ADC=∠DCB,EC=DF= ![]() DC,
DC,
∵在△ADF和△DCE中, 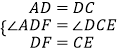 ,
,
∴△ADF≌△DCE(SAS),
∴∠AFD=∠DEC
∵∠DEC+∠CDE=90°
∴∠AFD+∠CDE=90°=∠DPF
∴AF⊥DE,∴①正确;
如图2,
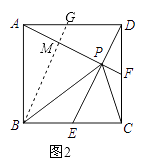
过B作BG∥DE交AD于G,交AP于M,
∵AF⊥DE,BG∥DE,E是BC中点,
∴BG⊥AP,G是AD的中点,
∴BG是AP的垂直平分线,
∴△ABP是等腰三角形
∴BP=AB=AD,∴②正确;
如图3,
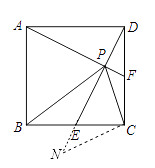
延长DE至N,使得EN=PF,连接CN,
∵∠AFD=∠DEC
∴∠CEN=∠CFP
又∵E,F分别是BC,DC的中点,
∴CE=CF,
∵在△CEN和△CFP中, 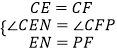 ,
,
∴△CEN≌△CFP(SAS),
∴CN=CP,∠ECN=∠PCF,
∵∠PCF+∠BCP=90°
∴∠ECN+∠BCP=∠NCP=90°
∴△NCP是等腰直角三角形
∴PN=PE+NE=PE+PF= ![]() PC,∴③正确,④错误;
PC,∴③正确,④错误;
∴①②③正确.
所以答案是:①②③.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.

【题目】如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中心重合,这样得到图②,图③,…
(1)观察图形并完成表格:
图形名称 | 基本图形的个数 | 菱形的个数 |
图① | 1 | 1 |
图② | 2 | 3 |
图③ | 3 | 7 |
图④ | 4 | |
… | … | … |
猜想:在图n中,菱形的个数为 [用含有n(n≥3)的代数式表示];
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1 , 1),则x1=;第2017个基本图形的中心O2017的坐标为 .
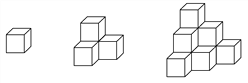
【题目】如图棱长为a的小正方体,按照下图的方法继续摆放,自上而下分别叫第一层、第二层…第n层,第n层的小正方体的个数记为S.解答下列问题:
n | 1 | 2 | 3 | 4 | … |
S | 1 | 3 | … |
(1)按要求填写上表:
(2)研究上表可以发现S随n的变化而变化,且S随n的增大而增大有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时,S的值为多少?