题目内容
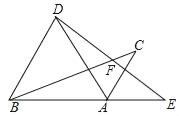
【题目】如图1,已知射线AP是∠MAN的角平分线,点B为射线AP上的一点且AB=10,过点B分别作BC⊥AM于点C,作BD⊥AN于点D,BC=6.
(1)在图1中连接CD交AB于点O.求证:AB垂直平分CD;
(2)从A,B两题中任选一题作答,我选择 题
A.将图1中的△ABC沿射线AP的方向平移得到△ABC,点A、B、C的对应点分别为A′、B′、C′.若平移后点B的对应点B′的位置如图2,连接DB′.
①请在图2中画出此时的△A′B′C′,并在图中标注相应的字母;
②若图2中的DB′∥A′C′,写出平移的距离.
B.将图1中的△ABC沿射线AP的方向平移得到△A′B′C′,点A、B、C的对应点分别为A′、B′、C′.
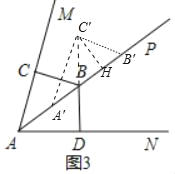
①在△A′B′C′平移的过程中,若点C′与点D的连线恰好经过点B,请在图3中画出此时的△A′B′C′,并在图中标注相应的字母;
②如图3,点C′与点D的连线恰好经过点B,写出此时平移的距离.
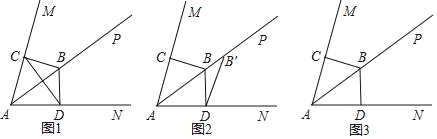
【答案】(1)证明见解析;(2)A:①△A′B′C′如图所示;见解析;②平移的距离为![]() ,B:①△A′B′C′如图所示:见解析;②平移的距离为
,B:①△A′B′C′如图所示:见解析;②平移的距离为![]() .
.
【解析】
(1)只要证明△ABC≌△ABD,即可推出AC=AD,BC=BD,可得AB垂直平分线段CD;(2)A:①作出△A′B′C′即可;②作DH⊥AB于H.首先证明DA=DB′,想办法求出AH即可解决问题;B:①作出△A′B′C′即可;②作C′H⊥AP于H.首先证明C′B=C′B′,想办法求出B′H即可解决问题.
(1)证明:如图1中,
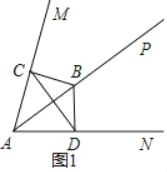
∵BC⊥AM,BD⊥AN,
∴∠ACB=∠ADB=90°,
∵∠BAC=∠BAD,AB=AB,
∴△ABC≌△ABD,
∴AC=AD,BC=BD,
∴AB垂直平分线段CD.
(2)A:①△A′B′C′如图所示;
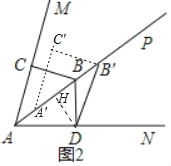
②作DH⊥AB于H.
在Rt△ABD中,AB=10,BD=BC=6,
∴AD=![]() =8,
=8,
∵cos∠DAH=![]() =
=![]() ,
,
∴AH=![]() ,
,
∵DB′∥AC,
∴∠AB′D=∠CAB,
∵∠CAB=∠DAB,
∴∠DAB=∠AB′D,
∴DA=DB′,∵DH⊥AB′,
∴AH=HB′,
∴AB′=![]() ,
,
∴BB′=AB′﹣AB=![]() ﹣10=
﹣10=![]() ,
,
∴平移的距离为![]() ,
,
B:①△A′B′C′如图所示:
②作C′H⊥AP于H.
∵∠ABD=∠C′BB′=∠C′B′A′,
∴C′B=C′B′,
∵C′H⊥BB′,
∴BH=HB′,
∵cos∠A′B′C′=![]() ,
,
∴![]() ,
,
∴HB′=![]() ,
,
∴BB′=2B′H=![]() ,
,
∴平移的距离为![]() .
.
故答案为A或B,![]() ,
,![]() .
.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案【题目】2015年3月30日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
频率分布表
分数段 | 频数 | 频率 |
50.5~60.5 | 16 | 0.08 |
60.5~70.5 | 40 | 0.2 |
70.5~80.5 | 50 | 0.25 |
80.5~90.5 | m | 0.35 |
90.5~100.5 | 24 | n |
(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?