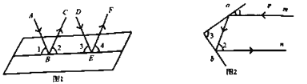题目内容
【题目】如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:
①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤S四边形AEPF= ![]() S△ABC .
S△ABC .
当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确的序号有 . 
【答案】①②③⑤
【解析】解:∵AB=AC,∠BAC=90°,点P是BC的中点,
∴∠EAP= ![]() ∠BAC=45°,AP=
∠BAC=45°,AP= ![]() BC=CP.①在△AEP与△CFP中,
BC=CP.①在△AEP与△CFP中,
∵∠EAP=∠C=45°,AP=CP,∠APE=∠CPF=90°﹣∠APF,
∴△AEP≌△CFP,∴AE=CF.正确;②由①知,△AEP≌△CFP,
∴∠APE=∠CPF.正确;③由①知,△AEP≌△CFP,
∴PE=PF.又∵∠EPF=90°,
∴△EPF是等腰直角三角形.正确;④只有当F在AC中点时EF=AP,故不能得出EF=AP,错误;⑤∵△AEP≌△CFP,同理可证△APF≌△BPE.
∴S四边形AEPF=S△AEP+S△APF=S△CPF+S△BPE= ![]() S△ABC.正确.
S△ABC.正确.
故正确的序号有①②③⑤.
【考点精析】根据题目的已知条件,利用全等三角形的性质和等腰三角形的性质的相关知识可以得到问题的答案,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等;等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
相关题目