题目内容
【题目】如图，已知△ABC中，AB=AC，∠A=100°，BD平分∠ABC，求证：BC=BD+AD．
【答案】见解析
【解析】
试题由题作辅助线，由BD平分∠ABC，∠1=∠2进而得△ABD≌△EBD∠DEB=∠A=100°，则得∠DEC=80°又∠2=20∴∠F=80；因为∠4=∠3=40°，所以△DCE≌△DCF（AAS）所以DF=DE=AD，可得BC=BF=BD+DF=BD+AD．
如图，在BC上截取BE=BA，延长BD到F使BF=BC，连接DE、CF．
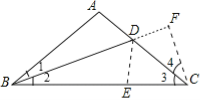
∵∠1=∠2，BD是公共边，BE=BA，
∴△ABD≌△EBD
∴∠DEB=∠A=100°，则得∠DEC=80°
∵AB=AC，BD平分∠ABC
∴∠1=∠2=20°，∠3=40°
∵BC=BF，∠2=20°，
∴∠F=∠FCB=
（180°-∠2）=80°则∠F=∠DEC
∴∠4=80°-∠3=40°，
∴∠3=∠4，∠F=∠DEC，
又∵DC=DC，
∴△DCE≌△DCF（AAS）
∴DF=DE=AD
∴BC=BF=BD+DF=BD+AD．
练习册系列答案
相关题目
