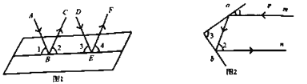题目内容
【题目】如图①，把∠α=60°的一个单独的菱形称作一个基本图形，将此基本图形不断的复制并平移，使得下一个菱形的一个顶点与前一个菱形的中心重合，这样得到图②，图③，…
（1）观察图形并完成表格：
图形名称 | 基本图形的个数 | 菱形的个数 |
图① | 1 | 1 |
图② | 2 | 3 |
图③ | 3 | 7 |
图④ | 4 | |
… | … | … |
猜想：在图n中，菱形的个数为 [用含有n（n≥3）的代数式表示]；
（2）如图，将图n放在直角坐标系中，设其中第一个基本图形的中心O1的坐标为（x1 ， 1），则x1=；第2017个基本图形的中心O2017的坐标为 ．
【答案】
（1）11,4n﹣5
（2）
,（2017 ,1）
【解析】解：（1）由题意可知，图③中菱形的个数7=3+4×（3﹣2），
图④中，菱形的个数为3+4×（4﹣2）=11，
∵当n≥3时，每多一个基本图形就会多出4个菱形，
∴图（n）中，菱形的个数为3+4（n﹣2）=4n﹣5，
（2）过点O1作O1A⊥y轴，O1B⊥x轴，则OA=1，
由菱形的性质知∠BAO1=30°，
∴AO1= 
= 
= ，
即x1= ，
中心O2的坐标为（2 ，1）、O3的坐标为（3 ，1）…，O2017的坐标为（2017 ，1），
故答案为：（1）11，4n﹣5；（2） ，（2017 ，1）．
（1）观察所给的图形可知从第3个图形开始，每多一个基本图形就会多出4个菱形；
（2）根据菱形的性质求得中心O1的坐标，然后再找出图中的规律，依据规律进行计算即可.
练习册系列答案
相关题目
