Question

【题目】如图，一次函数y=kx+b的图象l与坐标轴分别交于点E，F，与双曲线y=﹣ （x＜0）交于点P（﹣1，n），且F是PE的中点，直线x=a与l交于点A，与双曲线交于点B（不同于A），PA=PB，则a= ．

Answer 1

【答案】﹣2
【解析】解：∵双曲线y=﹣ （x＜0）经过点P（﹣1，n），

∴n=﹣ =9，

∴P（﹣1，9），

∵F是PE的中点，

∴OF= ×9=4.5，

∴F（0，4.5），

设直线l的解析式为y=kx+b，

∴ ，解得 ，

∴直线l的解析式为y=﹣4.5x+4.5；

过P作PD⊥AB，垂足为点D，

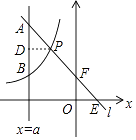
∵PA=PB，

∴点D为AB的中点，

又由题意知A点的纵坐标为﹣4.5a+4.5，B点的纵坐标为﹣ ，D点的纵坐标为9，

∴得方程﹣4.5a+4.5﹣ =9×2，

解得a1=﹣2，a2=16（舍去）．

∴当PA=PB时，a=﹣2，

所以答案是﹣2．