题目内容
【题目】如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,则旋转第2016次后,得到的等腰直角三角形的直角顶点P2017的坐标为( )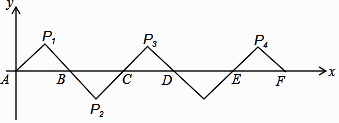
A.(4030,1)
B.(4029,﹣1)
C.(4033,1)
D.(4031,﹣1)
【答案】C
【解析】解:作P1⊥x轴于H,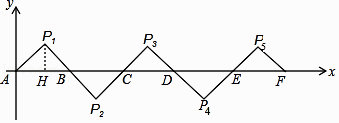
∵A(0,0),B(2,0),
∴AB=2,
∵△AP1B是等腰直角三角形,
∴P1H= ![]() AB=1,AH=BH=1,
AB=1,AH=BH=1,
∴P1的纵坐标为1,
∵△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D,
∴P2的纵坐标为﹣1,P3的纵坐标为1,P4的纵坐标为﹣1,P5的纵坐标为1,…,
∴P1017的纵坐标为1,横坐标为2017×2﹣1=4033,
即P1017(4033,1).
故选C.
作P1⊥x轴于H,利用等腰直角三角形的性质得P1H= ![]() AB=1,AH=BH=1,则P1的纵坐标为1,再利用旋转的性质易得P2的纵坐标为﹣1,P3的纵坐标为1,P4的纵坐标为﹣1,P5的纵坐标为1,…,于是可判断P1017的纵坐标为1,而横坐标为2017×2﹣1=4033,所以P1017(4033,1).
AB=1,AH=BH=1,则P1的纵坐标为1,再利用旋转的性质易得P2的纵坐标为﹣1,P3的纵坐标为1,P4的纵坐标为﹣1,P5的纵坐标为1,…,于是可判断P1017的纵坐标为1,而横坐标为2017×2﹣1=4033,所以P1017(4033,1).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目