题目内容
【题目】如图,抛物线y=ax2+bx+1与直线y=﹣ax+c相交于坐标轴上点A(﹣3,0),C(0,1)两点.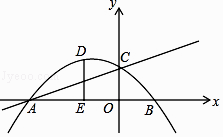
(1)直线的表达式为;抛物线的表达式为 .
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交直线AC于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)P为抛物线上一动点,且P在第四象限内,过点P作PN垂直x轴于点N,使得以P、A、N为顶点的三角形与△ACO相似,请直接写出点P的坐标.
【答案】
(1)y= ![]() x+1;y=﹣
x+1;y=﹣ ![]() x2﹣
x2﹣ ![]() x+1
x+1
(2)
解:∵点D在抛物线在第二象限部分上的一点,
∴可设D(t,﹣ ![]() t2﹣
t2﹣ ![]() t+1),则F(t,
t+1),则F(t, ![]() t+1),
t+1),
∴DF=﹣ ![]() t2﹣
t2﹣ ![]() t+1﹣(
t+1﹣( ![]() t+1)=﹣
t+1)=﹣ ![]() t2﹣t=﹣
t2﹣t=﹣ ![]() (t+
(t+ ![]() )2+
)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴当t=﹣ ![]() 时,DF有最大值,最大值为
时,DF有最大值,最大值为 ![]() ,此时D点坐标为(﹣
,此时D点坐标为(﹣ ![]() ,
, ![]() )
)
(3)
解:设P(m,﹣ ![]() m2﹣
m2﹣ ![]() m+1),如图2,
m+1),如图2,
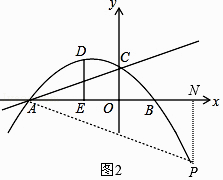
∵P在第四象限,
∴m>0,﹣ ![]() m2﹣
m2﹣ ![]() m+1<0,
m+1<0,
∴AN=m+3,PN= ![]() m2+
m2+ ![]() m﹣1,
m﹣1,
∵∠AOC=∠ANP=90°,
∴当以P、A、N为顶点的三角形与△ACO相似时有△AOC∽△PNA和△AOC∽△ANP,
①当△AOC∽△PNA时,则有 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得m=﹣3或m=10,经检验当m=﹣3时,m+3=0,
∴m=10,此时P点坐标为(10,﹣39);
②当△AOC∽△ANP时,则有 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得m=2或m=﹣3,经检验当m=﹣3时,m+3=0,
∴m=2,此时P点坐标为(3,﹣ ![]() );
);
综上可知P点坐标为(10,﹣39)或(3,﹣ ![]() )
)
【解析】解:(1)把A、C两点坐标代入直线y=﹣ax+c可得 ![]() ,解得
,解得 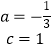 ,
,
∴直线的表达式为y= ![]() x+1,
x+1,
把A点坐标和a=﹣ ![]() 代入抛物线解析式可得9×(﹣
代入抛物线解析式可得9×(﹣ ![]() )﹣3b+1=0,解得b=﹣
)﹣3b+1=0,解得b=﹣ ![]() ,
,
∴抛物线的表达式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+1,
x+1,
所以答案是:y= ![]() x+1;y=﹣
x+1;y=﹣ ![]() x2﹣
x2﹣ ![]() x+1;
x+1;

 名校课堂系列答案
名校课堂系列答案