题目内容
【题目】如图，一艘海警船在A处发现北偏东30°方向相距12海里的B处有一艘可疑货船，该艘货船以每小时10海里的速度向正东航行，海警船立即以每小时14海里的速度追赶，到C处相遇，求海警船用多长时间追上了货船？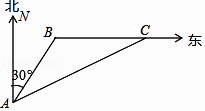
【答案】解：如图，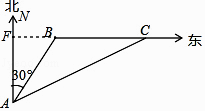
由题意，∠BAF=30°，∠CAF=60°，
∴∠FBA=60°，∠BAC=∠C=30°，
∴BC=AB=12，
货轮从出发到客轮相逢所用的时间= 
=1.2小时．
答：货轮从出发到客轮相逢所用的时间1，2小时．
【解析】首先证明AB=BC=12，根据时间=路程÷速度，计算即可解决问题．
【考点精析】认真审题，首先需要了解关于方向角问题(指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角)．
练习册系列答案
优学名师名题系列答案
相关题目
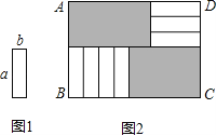
【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形后，将其裁成四个相同的等腰梯形（如图1），然后拼成一个平行四边形（如图2）。那么通过计算两个图形的阴影部分的面积，可以验证成立的公式是（ ）
A．a2－b2=(a－b)2 | B．(a+b)2="a+2ab+b" |
C．(a－b)2=a2－2ab+b2 | D．a2－b2=(a－b)(a+b) |
