题目内容
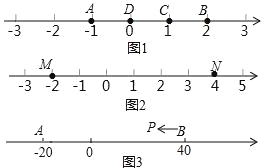
【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
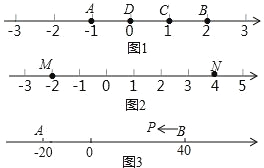
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
【答案】(1)点D是(B,C)的奇异点,不是(A,B)的奇异点;(2)(M,N)的奇异点表示的数是2;(3)①点P表示的数是0或10或20时,P、A、B中恰有一个点为其余两点的奇异点;②PB=120或180或90.
【解析】
(1)根据奇异点的定义和数轴上两点间的距离,即可求出点D到点A的距离为1,到点B的距离为2,以及点D到点C的距离为1,就可以对点D做出判断.
(2)设奇异点表示的数为x,根据奇异点的定义可得方程:x﹣(﹣2)=2(4﹣x).从而求得x值.
(3)①当P在A、B两点之间时,P、A、B中恰有一个点为其余两点的奇异点需分类讨论,具体分四种情况讨论:当点P是(A,B)的奇异点时、当点P是(B,A)的奇异点时、当点A是(B,P)的奇异点时、当点B是(A,P)的奇异点时,计算方法同(1).
②点P到达点A后继续向左运动,是否存在使得P、A、B中恰有一个点为其余两点的奇异点的情况方法同①分四种情况讨论:当点P为(B,A)的奇异点时,PB=120;
当点A为(P,B)的奇异点时,PB=180;当点A为(B,P)的奇异点时,PB=90;
当点B为(P,A)的奇异点时,PB=120.
(1)在图1中,点D到点A的距离为1,到点B的距离为2,
∴点D是(B,C)的奇异点,不是(A,B)的奇异点;
(2)设奇异点表示的数为x,
则由题意,得x﹣(﹣2)=2(4﹣x).
解得x=2.
∴(M,N)的奇异点表示的数是2;
(3)①设点P表示的数为y.
当点P是(A,B)的奇异点时,
则有y+20=2(40﹣y),
解得y=20.
当点P是(B,A)的奇异点时,
则有40﹣y=2(y+20),
解得y=0.
当点A是(B,P)的奇异点时,
则有40+20=2(y+20),
解得y=10.
当点B是(A,P)的奇异点时,
则有40+20=2(40﹣y),解得y=10.
∴当点P表示的数是0或10或20时,
P、A、B中恰有一个点为其余两点的奇异点.
②当点P为(B,A)的奇异点时,PB=120;
当点A为(P,B)的奇异点时,PB=180;
当点A为(B,P)的奇异点时,PB=90;
当点B为(P,A)的奇异点时,PB=120.