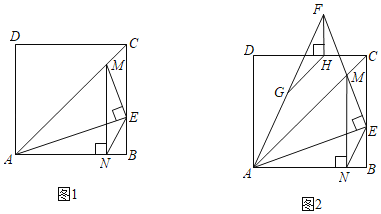题目内容
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
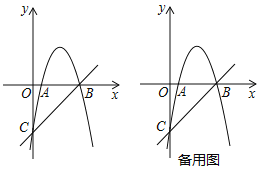
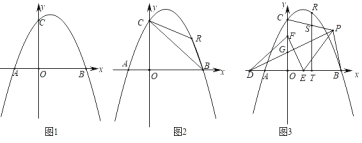
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
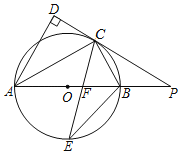
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
【答案】(1)y=﹣![]() x2+x+4;(2)s=﹣t2+4t;(3)当a=1时,R(2,4),当a=
x2+x+4;(2)s=﹣t2+4t;(3)当a=1时,R(2,4),当a=![]() 时,R(
时,R(![]() ,
,![]() ).
).
【解析】
(1)由题意可求A(-2,0),B(4,0),将A点代入y=ax2-2ax+4,即可求a的值;
(2)设R(t,﹣![]() t2+t+4),过点R作x、y轴的垂线,垂足分别为R',R',可得四边形RR'OR'是矩形,求出S△OCR=
t2+t+4),过点R作x、y轴的垂线,垂足分别为R',R',可得四边形RR'OR'是矩形,求出S△OCR=![]() OCRR'=
OCRR'=![]() ×4t=2t,S△ORB=
×4t=2t,S△ORB=![]() OBRR'=
OBRR'=![]() ×4(﹣
×4(﹣![]() t2+t+4)=﹣t2+2t+8,则有S△RBC=S△ORB+S△OCR﹣S△OBC=﹣t2+2t+8+2t﹣
t2+t+4)=﹣t2+2t+8,则有S△RBC=S△ORB+S△OCR﹣S△OBC=﹣t2+2t+8+2t﹣![]() ×4×4=﹣t2+4t;
×4×4=﹣t2+4t;
(3)设EF、PD交于点G',连EG,可证明OP是EG的垂直平分线,过P作KP⊥x轴于K,PW⊥y轴于W,交RT于点H,则四边形PWOK是正方形,设OT=2a,则TK=KB=CW=2﹣a,HT=OK=PW=2+a,可求HS=TS﹣HT=![]() ﹣(2+a)=
﹣(2+a)=![]() ﹣a,又由tan∠HPS=
﹣a,又由tan∠HPS=![]() ,可得
,可得 ,则a=1或a=
,则a=1或a=![]() ,即可求R得坐标.
,即可求R得坐标.
解:(1)∵抛物线的对称轴为x=1,AB=6,
∴A(﹣2,0),B(4,0),
将点A代入y=ax2﹣2ax+4,则有0=4a+4a+4,
∴a=﹣![]() ,
,
∴y=﹣![]() x2+x+4;
x2+x+4;
(2)
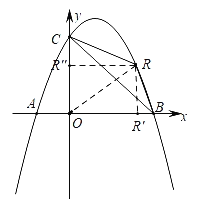
设R(t,﹣![]() t2+t+4),
t2+t+4),
过点R作x、y轴的垂线,垂足分别为R',R',
则∠RR'O=∠RR'O=∠R'OR'=90°,
∴四边形RR'OR'是矩形,
∴RR'=OR'=t,OR'=RR'=﹣![]() t2+t+4,
t2+t+4,
∴S△OCR=![]() OCRR'=
OCRR'=![]() ×4t=2t,
×4t=2t,
S△ORB=![]() OBRR'=
OBRR'=![]() ×4(﹣
×4(﹣![]() t2+t+4)=﹣t2+2t+8,
t2+t+4)=﹣t2+2t+8,
∴S△RBC=S△ORB+S△OCR﹣S△OBC=﹣t2+2t+8+2t﹣![]() ×4×4=﹣t2+4t;
×4×4=﹣t2+4t;
(3)
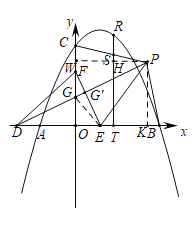
设EF、PD交于点G',连EG,
∵PD⊥EF,
∴∠FG'G=∠DG'E=90°=∠DOG,
∴∠OFE=∠GDO,
∵∠DGO=∠FOE=90°,EF=DG,
∴OP是EG的垂直平分线,
∴OP平分∠COB,
过P作KP⊥x轴于K,PW⊥y轴于W,交RT于点H,
则PW=PK,∠PWO=∠PKO=∠WOK=90°,
∴四边形PWOK是正方形,
∴WO=OK,
∵OC=OB=4,
∴CW=KB,
∵P在BT垂直平分线上,
∴PT=PB,
∴TK=KB=CW,
设OT=2a,则TK=KB=CW=2﹣a,
HT=OK=PW=2+a,
∵OB﹣TS=![]() ,
,
∴HS=TS﹣HT=![]() ﹣(2+a)=
﹣(2+a)=![]() ﹣a,
﹣a,
∵tan∠HPS=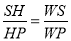 ,
,
∴ ,
,
∴a=1或a=![]() ,
,
当a=1时,OT=2,∴R(2,4),
当a=![]() 时,OT=
时,OT=![]() ,∴R(
,∴R(![]() ,
,![]() )
)
综上,点R的坐标是(2,4),(![]() ,
,![]() ).
).