题目内容
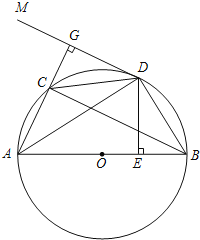
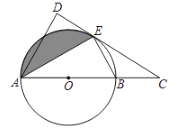
【题目】如图,AB 是⊙O的直径,∠DAB的角平分线AC交⊙O于点C,过点C作CD⊥AD于D,AB的延长线与DC的延长线相交于点P,∠ACB的角平分线CE交AB于点F、交⊙O于E.
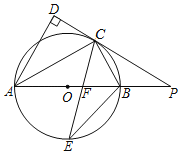
(1)求证:PC与⊙O相切;
(2)求证:PC=PF;
(3)若AC=8,tan∠ABC=![]() ,求线段BE的长.
,求线段BE的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
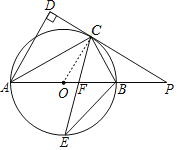
(1)如图,连接OC,根据AC是∠DAB的角平分线,证明OC∥AD,进而可证PC与⊙O相切;
(2)根据CF是∠ACB的角平分线,和外角定义即可得∠PFC=∠PCF,进而得PC=PF;
(3)根据AB 是⊙O的直径,可得∠ACB=90°,根据AC=8,tan∠ABC=![]() =
=![]() ,可得BC=6,再根据勾股定理和垂径定理即可得线段BE的长.
,可得BC=6,再根据勾股定理和垂径定理即可得线段BE的长.
(1)如图,连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵AC是∠DAB的角平分线,
∴∠DAC=∠OAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴PC与⊙O相切;
(2)∵CF是∠ACB的角平分线,
∴∠ACF=∠BCF,
∵∠CAF=∠PCB,
∴∠ACF+∠CAF=∠BCF+∠PCB,
∴∠PFC=∠PCF,
∴PC=PF.
(3)∵AB 是⊙O的直径,
∴∠ACB=90°,
∵AC=8,tan∠ABC=![]() =
=![]() ,
,
∴BC=6,
∴AB=![]() =10,
=10,
∴OB=OE=5,
∵∠ACE=∠BCE,
∴![]() ,
,
∴EO⊥AB,
∴BE=![]() =5
=5![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目