题目内容
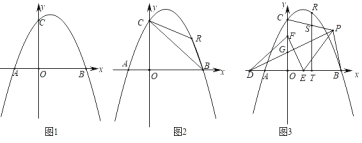
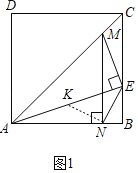
【题目】如图1,在正方形ABCD中,点E是边BC上一点,连接AE,过点E作EM⊥AE,交对角线AC于点M,过点M作MN⊥AB,垂足为N,连接NE.
(1)求证:AE=![]() NE+ME;
NE+ME;
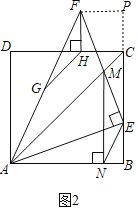
(2)如图2,延长EM至点F,使EF=EA,连接AF,过点F作FH⊥DC,垂足为H.
猜想CH与FH存在的数量关系,并证明你的结论;
(3)在(2)的条件下,若点G是AF的中点,连接GH.当GH=CH时,直接写出GH与AC之间存在的数量关系.
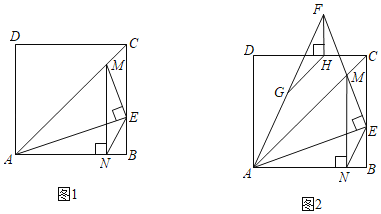
【答案】(1)见解析;(2)![]() ,见解析;(3)
,见解析;(3)![]()
【解析】
(1)如图1,过点N作NK⊥NE,交AE于点K.再证明△ANK≌△MNE得到,AK=ME,NK=NE,再根据正方形的性质即可证明;
(2)过点F作FP⊥BC,交BC的延长线于点P.可得∠P=∠PCH=∠CHF=90°,即四边形PCHF是矩形.再证明△ABE≌△EPF,可得BE=PF,AB=EP.即CP=BE=PF.可以说明矩形PCHF是正方形即可说明理由;
(3)延长FH交AC于点Q,由中位线定理可得出AQ=2GH,由等腰直角三角形的性质可得出CQ=![]() GH即可.
GH即可.
(1)证明:如图1,过点N作NK⊥NE,交AE于点K.
∴∠KNE=90°.
∵MN⊥AB,
∴∠MNA=90°.
∴∠ANK=∠MNE.
∵ME⊥AE,
∴∠AEM=∠ANM=90°.
∴∠NAK=∠NME.
∵四边形ABCD是正方形,∠ANM=90°.
∴∠MAN=∠NMA=45°.
∴AN=MN.
在△ANK和△MNE中,
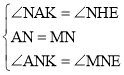 ,
,
∴△ANK≌△MNE(ASA).
∴AK=ME,NK=NE.
∴KE=![]() NE.
NE.
∴AE=AK+KE=ME+![]() NE.
NE.
(2)解:CH=FH,理由如下:
如图2,过点F作FP⊥BC,交BC的延长线于点P.
∴∠P=90°.
∵∠BAE+∠AEB=∠FEP+∠AEB=90°,
∴∠BAE=∠FEP.
∵四边形ABCD是正方形,
∴∠B=∠BCD=∠PCD=90°,AB=BC.
∵FH⊥CD,
∴∠FHC=90°.
∴∠P=∠PCH=∠CHF=90°.
∴四边形PCHF是矩形.
在△ABE和△EPF中,
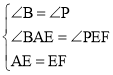 ,
,
∴△ABE≌△EPF(AAS).
∴BE=PF,AB=EP.
∵AB=BC,
∴EP=BC.
∴CP=BE=PF.
∴矩形PCHF是正方形.
∴FH=CH.
(3)AC=![]() GH,理由如下:
GH,理由如下:
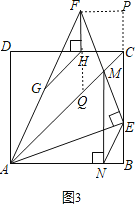
如图3,延长FH交AC于点Q,
在正方形ABCD中,∠ACD=45°,
∵∠FHC=90°,
∴∠HQC=∠HCQ=45°,
∴CH=HQ,CQ=![]() CH,
CH,
∵CH=FH,
∴HQ=FH,
∵G是AF的中点,
∴GH=![]() AQ,
AQ,
又∵GH=CH,
∴CQ=![]() GH,
GH,
∴AC=AQ+CQ=2GH+![]() GH=(2+
GH=(2+![]() )GH.
)GH.

【题目】随着时代的不断发展,新颖的网络购进逐渐融入到人们的生活中,“拼一拼”电商平台上提供了一种拼团购买方式,当拼团(单数不超过15单)成功后商家将会让利一定的额度给予顾客实惠.现在某商家准备出手一种每件成本25元/件的新产品,经市场调研发现,单价y(单位:元)、日销售量m(单位:件)与拼单数x(单位:单)之间存在着如表的数量关系:
拼单数x(单位:单) | 2 | 4 | 8 | 12 |
单价y(单位:元) | 34.50 | 34.00 | 33.00 | 32.00 |
日销售量m(单位:件) | 68 | 76 | 92 | 108 |
请根据以上提供的信息解决下列问题:
(1)请直接写出单价y和日销售量m分别与拼单数x之间的一次函数关系式;
(2)拼单数设置为多少单时的日销售利润最大,最大的销售利润是多少?
(3)在实际销售过程中,厂家希望能有更多的商品出售,因此对电商每销售一件商品厂家就给予电商补助a元(a≤2),那么电商在获得补助之日后日销售利润能够随单数x的增大而增大,那么a的取值范围是什么?
【题目】甲、乙两个芭蕾舞团演员的身高(单位:cm)如下表:
甲 | 164 | 164 | 165 | 165 | 166 | 166 | 167 | 167 |
乙 | 163 | 163 | 165 | 165 | 166 | 166 | 168 | 168 |
两组芭蕾舞团演员身高的方差较小的是______.(填“甲”或“乙”)