题目内容
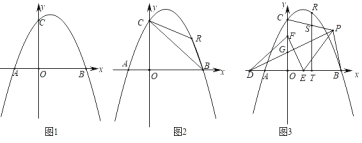
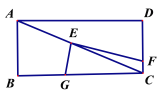
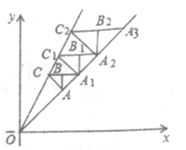
【题目】如图,在平面直角坐标系第一象限内,直线![]() 与直线
与直线![]() 的内部作等腰
的内部作等腰![]() ,使
,使![]() ,边
,边![]() 轴,
轴,![]() 轴,
轴,![]() 在直线
在直线![]() 上,点C在直线
上,点C在直线![]() 上,CB的延长线交直线
上,CB的延长线交直线![]() 于点
于点![]() ,作等腰
,作等腰![]() ,使
,使![]() 轴,
轴,![]() 轴,点
轴,点![]() 在直线
在直线![]() 上,按此规律,则等腰
上,按此规律,则等腰![]() 的腰长为_______.
的腰长为_______.
【答案】![]()
【解析】
设AB=a,利用两个函数解析式求出点B、C的坐标,然后求出AB的长度,再根据B1C1∥x轴,A1B1∥y轴,利用y=x求出A11点的坐标,A1B1=b,则利用y=2x求出点C1(![]() ,
,![]() ),从而得到A1B1的长度,以此类推,求出A2B2、A3B3,从而得出
),从而得到A1B1的长度,以此类推,求出A2B2、A3B3,从而得出![]() 即可得到结果.
即可得到结果.
解:设![]() ,
,
![]() 直线
直线![]() 与直线
与直线![]() 的内部作等腰
的内部作等腰![]() ,是
,是![]() ,边
,边![]() 轴,
轴,![]() 轴,点
轴,点![]() 在直线
在直线![]() 上,
上,
![]() ,
,![]() ,
,![]() ,
,
![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
解得![]() ,
,
![]() 等腰
等腰![]() 的腰长为
的腰长为![]() ,
,
![]() ,
,![]() ,
,
![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]()
![]()
解得![]() ,
,
![]() 等腰
等腰![]() △
△![]() 的腰长为
的腰长为![]()
![]() ,
,![]()
![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]()
![]() ,
,
解得![]() ,
,
![]() 等腰
等腰![]() △
△![]() 的腰长为
的腰长为![]() ,
,
以此类推,
![]() ,即等腰
,即等腰![]() △
△![]() 的腰长为
的腰长为![]() ,
,
![]() ,即等腰
,即等腰![]() △
△![]() 的腰长为
的腰长为![]() ,
,
![]()
![]() ,等腰
,等腰![]() △
△![]() 的腰长为
的腰长为![]() ,
,
∴![]() 的腰长为
的腰长为![]() .
.
故答案为![]() .
.

【题目】甲、乙两个芭蕾舞团演员的身高(单位:cm)如下表:
甲 | 164 | 164 | 165 | 165 | 166 | 166 | 167 | 167 |
乙 | 163 | 163 | 165 | 165 | 166 | 166 | 168 | 168 |
两组芭蕾舞团演员身高的方差较小的是______.(填“甲”或“乙”)
【题目】某制药厂需要紧急生产一批能有效缓解“新冠肺炎”的药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量![]() (吨)是时间
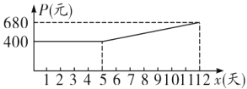
(吨)是时间![]() (天)的一次函数,且满足如下表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本
(天)的一次函数,且满足如下表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本![]() (元)与时间
(元)与时间![]() (天)的关系满足如图所示的函数图象.
(天)的关系满足如图所示的函数图象.
时间 | 2 | 4 |
每天产量 | 24 | 28 |
(1)求药品每天的产量![]() (吨)与时间
(吨)与时间![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)当![]() 时,直接写出
时,直接写出![]() (元)与时间
(元)与时间![]() (天)的函数关系是
(天)的函数关系是![]() ;
;
(3)若这批药品的价格为1400元/吨,每天的利润设为![]() 元,求哪一天的利润最高,最高利润是多少?(利润
元,求哪一天的利润最高,最高利润是多少?(利润![]() 售价
售价![]() 成本)
成本)