题目内容
【题目】定义:对于平面直角坐标系![]() 中的线段
中的线段![]() 和点
和点![]() ,在
,在![]() 中,当
中,当![]() 边上的高为2时,称
边上的高为2时,称![]() 为
为![]() 的“等高点”,称此时
的“等高点”,称此时![]() 为
为![]() 的“等高距离”.
的“等高距离”.
(1)若点![]() 的坐标为(1,2),点
的坐标为(1,2),点![]() 的坐标为(4,2),则在点
的坐标为(4,2),则在点![]() (1,0),
(1,0),![]() (
(![]() ,4),
,4),![]() (0,3)中,
(0,3)中,![]() 的“等高点”是点___;
的“等高点”是点___;
(2)若![]() (0,0),
(0,0),![]() =2,当
=2,当![]() 的“等高点”在
的“等高点”在![]() 轴正半轴上且“等高距离”最小时,点
轴正半轴上且“等高距离”最小时,点![]() 的坐标是__.
的坐标是__.
【答案】A或B 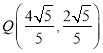 或
或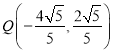
【解析】
(1)根据“等高点”的概念解答即可;
(2)先证明“等高距离”最小时△MPQ为等腰三角形,再利用勾股定理求出点Q坐标即可.
(1)①∵P(1,2),Q(4,2),
∴在点A(1,0),B(![]() ,4)到PQ的距离为2.
,4)到PQ的距离为2.
∴PQ的“等高点”是A或B,
故答案为:A或B;
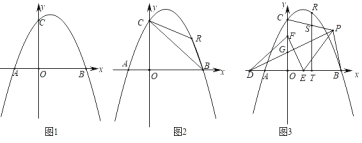
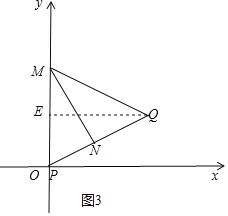
(2)如图2,过PQ的“等高点”M作MN⊥PQ于点N,
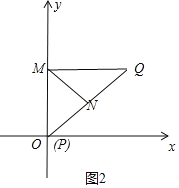
∴PQ=2,MN=2.
设PN=x,则NQ=2-x,
在Rt△MNP和Rt△MNQ中,由勾股定理得:
MP2=22+x2=4+x2,MQ2=22+(2-x)2=x2-4x+8,
∴MP2+MQ2=2x2-4x+12=2(x-1)2+10,
∵MP2+MQ2≤(MP+MQ)2,
∴当MP2+MQ2最小时MP+MQ也最小,此时x=1,
即PN=NQ,
∴△MPQ为等腰三角形,
∴MP=MQ=![]() ,
,
如图3,设Q坐标为(x,y),过点Q作QE⊥y轴于点E,
则在Rt△MNP和Rt△MNQ中由勾股定理得:
QE2=QP2-OE2=22-y2=4-y2,QE2=QM2-ME2=![]() ,
,
∴![]() ,
,
解得y=![]() ,
,
QE2=4-y2=4-(![]() )2=
)2=![]() ,
,
当点Q在第一象限时x![]() ,当点Q在第二象限时x
,当点Q在第二象限时x![]() ,
,
∴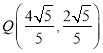 或
或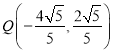 ,
,
故答案为: 或
或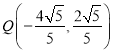 .
.

 智慧小复习系列答案
智慧小复习系列答案【题目】随着时代的不断发展,新颖的网络购进逐渐融入到人们的生活中,“拼一拼”电商平台上提供了一种拼团购买方式,当拼团(单数不超过15单)成功后商家将会让利一定的额度给予顾客实惠.现在某商家准备出手一种每件成本25元/件的新产品,经市场调研发现,单价y(单位:元)、日销售量m(单位:件)与拼单数x(单位:单)之间存在着如表的数量关系:
拼单数x(单位:单) | 2 | 4 | 8 | 12 |
单价y(单位:元) | 34.50 | 34.00 | 33.00 | 32.00 |
日销售量m(单位:件) | 68 | 76 | 92 | 108 |
请根据以上提供的信息解决下列问题:
(1)请直接写出单价y和日销售量m分别与拼单数x之间的一次函数关系式;
(2)拼单数设置为多少单时的日销售利润最大,最大的销售利润是多少?
(3)在实际销售过程中,厂家希望能有更多的商品出售,因此对电商每销售一件商品厂家就给予电商补助a元(a≤2),那么电商在获得补助之日后日销售利润能够随单数x的增大而增大,那么a的取值范围是什么?