题目内容
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 图像上的一个动点,连接
图像上的一个动点,连接![]() ,若将线段
,若将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,则过点
,则过点![]() 的反比例函数解析式为__________.
的反比例函数解析式为__________.
【答案】![]()
【解析】
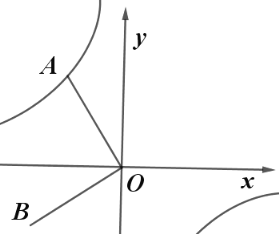
设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,得到AC=n,OC=-m,根据全等三角形的性质得到AC=OD=n,CO=BD=-m,于是得到结论.
∵点A是反比例函数![]() 的图象上的一个动点,设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,
的图象上的一个动点,设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,
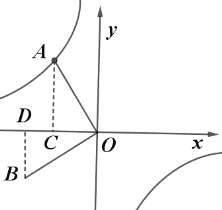
∴AC=n,OC=-m,
∴∠ACO=∠BDO=90°,
∵∠AOB=90°,
∴∠CAO+∠AOC=∠AOC+∠BOD=90°,
∴∠CAO=∠BOD,
在△ACO与△ODB中
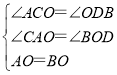 ,
,
∴△ACO≌△ODB,
∴AC=OD=n,CO=BD=-m,
∴B(-n,m),
∵mn=-4,
∴m(-n)=4,、
∴点B所在图象的函数表达式为![]() ,
,
故答案为:![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】甲、乙两个芭蕾舞团演员的身高(单位:cm)如下表:
甲 | 164 | 164 | 165 | 165 | 166 | 166 | 167 | 167 |
乙 | 163 | 163 | 165 | 165 | 166 | 166 | 168 | 168 |
两组芭蕾舞团演员身高的方差较小的是______.(填“甲”或“乙”)