题目内容
【题目】为了弘扬传统文化,某校组织八年级全体学生参加“恰同学少年,品诗词美韵”的古诗词比赛.比赛结束后,学校随机抽取的部分学生成绩作为样本,并进行整理后分成下面5组,![]() 分
分![]() 的小组称为“诗词少年”组,
的小组称为“诗词少年”组,![]() 分
分![]() 的小组称为“诗词居士”组,
的小组称为“诗词居士”组,![]() 分
分![]() 的小组称为“诗词圣手”组,
的小组称为“诗词圣手”组,![]() 分
分![]() 的小组称为“诗词达人”组,
的小组称为“诗词达人”组,![]() 分
分![]() 的小组称为“诗词泰斗”组;下面是将整理的样本绘制的不完整的频数分布直方图,请结合提供的信息解答下列问题:
的小组称为“诗词泰斗”组;下面是将整理的样本绘制的不完整的频数分布直方图,请结合提供的信息解答下列问题:
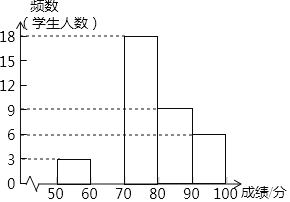
(1)若“诗词泰斗”组成绩的频率12.5%,求出样本容量,补全频数分布直方图;
(2)以各组组中值代表本组的选手的平均成绩,计算样本中不含“诗词圣手”组的其他四组学生的平均成绩;
(3)学校决定对成绩进人“诗词圣手”、“诗词达人”、“诗词泰斗“组的学生进行奖励,若八年级共有240名学生,请通过计算推断,大约有多少名学生获奖.
【答案】(1)48;补全图形见解析;(2)76分;(3)可以估计大约共有165名学生获奖
【解析】
(1)由题意先根据90~100分的人数及其所占百分比求得总人数,再由各组人数之和等于总人数求得60~70分的人数.从而补全图形;
(2)由题意值即根据平均数的定义进行分析求解可得;
(3)根据题意值即利用样本估计总体的思想进行分析运算求解即可.
解:(1) ∵被调查的总人数为![]() (名)
(名)
∴60~70分的人数为![]() (名)
(名)
所以样本容量为48,频数分布直方图如下:

(2)![]() (分),
(分),
即样本中不含“诗词圣手”组的其他四组学生的平均成绩为76分.
(3)因为![]() (名)
(名)
所以可以估计大约共有165名学生获奖.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】成都市某公司自主设计了一款可控温杯,每个生产成本为16元,投放市场进行了试销.经过调查得到每月销售量y(万个)与销售单价x(元/个)之间关系是一次函数的关系,部分数据如下:
销售单价x(元/个) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万个) | … | 60 | 50 | 40 | 30 | … |
(1)求y与x之间的函数关系;
(2)该公司既要获得一定利润,又要符合相关部门规定(一件产品的利润率不得高于50%)请你帮助分析,公司销售单价定为多少时可获利最大?并求出最大利润.