题目内容
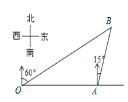
【题目】如图，港口A在观测站O的正东方向，OA=6，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离(即AB的长)为________．
【答案】
【解析】
过点A作AD⊥OB于D．先解Rt△AOD，得出AD=
OA=3，再由△ABD是等腰直角三角形，得出BD=AD=3，则AB=
AD=．
解：如图，过点A作AD⊥OB于D．
在Rt△AOD中，
∵∠ADO=90°，∠AOD=30°，OA=6，
∴AD=OA=3．
在Rt△ABD中，
∵∠ADB=90°，∠B=∠CAB-∠AOB=75°
30°=45°，
∴BD=AD=3，
∴AB=AD=．
即该船航行的距离（即AB的长）为km．
故答案为：．
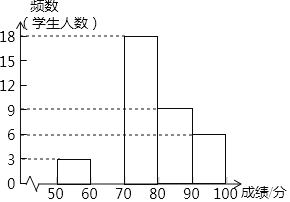
【题目】某校开展“传统文化”知识竞赛，已知该校七年级男生和女生各有学生200人，从中各随机抽取20名学生进行抽样调查，获得了他们知识竞赛成绩（满分100分），并进行整理，得到下面部分信息．
男生：74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74
女生：76 87 93 65 78 94 89 68 95 54 89 87 89 89 77 94 86 87 92 91
成绩 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
男生 | 0 | 1 | 10 | 1 | 8 |
女生 | 1 | 2 | a | 8 | 6 |
平均数、中位数、众数、方差如表所示：
成绩 | 平均数 | 中位数 | 众数 | 方差 |
男生 | 84 | 77 | 74 | 145.4 |
女生 | 84 | b | 89 | 115.6 |
根据以上信息，回答下列问题：
（1）a＝ ，b＝ ；
（2）你认为七年级学生中，男生还是女生的总体成绩较好，为什么？（至少从两个不同的角度说明）
（3）若在此次竞赛中，该校七年级学生中有四人取得100分的好成绩，且恰好是两个男生两个女生．现从这四人中随机抽取两人参加市里的竞赛，求这两人恰好是一男一女的概率．
