题目内容
【题目】某服装厂生产某品牌的T恤衫成本是每件10元。根据市场调查，以单价13元批发给经销，商销商愿意经销5000件，并且表示每降价0.1元，愿意多经销500件。服装厂决定批发价在不低于11.4元的前提下，将批发价下降0.1x元.
（1）求销售量y与x的关系，并求出x的取值范围；
（2）不考虑其他因素，请问厂家批发单价是多少时所获利润W可以最大？最大利润为多少？
【答案】（1）
，
；（2）批发单价是12元时所获利润W可以最大，最大利润为20000元.
【解析】
（1）根据销售量=原销量+多经销的销量即可列出函数关系式，根据批发价在不低于11.4元，可得x的取值范围；
（2）根据利润W=销量×单利润即可列出函数关系式，将函数化为顶点式，根据顶点式求最值即可.
解：（1）根据题意：，
因为批发价在不低于11.4元,所以
，解得
，
又
，所以.
所以销售量y与x的关系为：，x的取值范围为；
（2）根据题意：
因为-50＜0，所以当x=10时（在x取值范围之内），利润最大为20000元.
因为当x=10时，13-0.1x=12元
所以当批发单价是12元时所获利润W可以最大，最大利润为20000元.
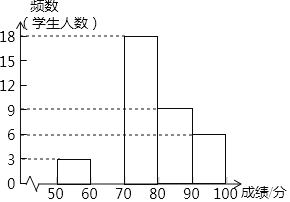
【题目】某校开展“传统文化”知识竞赛，已知该校七年级男生和女生各有学生200人，从中各随机抽取20名学生进行抽样调查，获得了他们知识竞赛成绩（满分100分），并进行整理，得到下面部分信息．
男生：74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74
女生：76 87 93 65 78 94 89 68 95 54 89 87 89 89 77 94 86 87 92 91
成绩 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
男生 | 0 | 1 | 10 | 1 | 8 |
女生 | 1 | 2 | a | 8 | 6 |
平均数、中位数、众数、方差如表所示：
成绩 | 平均数 | 中位数 | 众数 | 方差 |
男生 | 84 | 77 | 74 | 145.4 |
女生 | 84 | b | 89 | 115.6 |
根据以上信息，回答下列问题：
（1）a＝ ，b＝ ；
（2）你认为七年级学生中，男生还是女生的总体成绩较好，为什么？（至少从两个不同的角度说明）
（3）若在此次竞赛中，该校七年级学生中有四人取得100分的好成绩，且恰好是两个男生两个女生．现从这四人中随机抽取两人参加市里的竞赛，求这两人恰好是一男一女的概率．
