��Ŀ����
����Ŀ���ڵ�����ABC�У�AB=AC=5��BC=6������M��N�ֱ�������AB��AC�ϣ�M����A��B�غϣ�N����A��C�غϣ�����MN��BC������AMN��MN���ڵ�ֱ���۵���ʹ��A�Ķ�Ӧ��ΪP��
��1����MNΪ��ֵʱ����Pǡ������BC�ϣ�
��2����MN=x����MNP�������ABC�ص����ֵ����Ϊy����д��y��x�ĺ�����ϵʽ����xΪ��ֵʱ��y��ֵ������ֵ�Ƕ��٣�
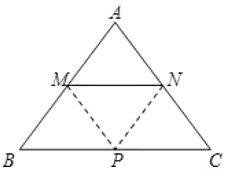
���𰸡���1����MN=3ʱ����Pǡ������BC�ϣ���2����x=4ʱ��y��ֵ������ֵ��4��
��������
��1������AP����MN��O��֤��AMN�ס�ABC��AO��MN����![]() ����MN��������2������A��AD��BC��D����MN��O��֤��AMN�ס�ABC��P��BC����AMN�ס�ABC����PEF�ס�PMN�ס�AMN�������������ʵ�y=S����MNFE=
����MN��������2������A��AD��BC��D����MN��O��֤��AMN�ס�ABC��P��BC����AMN�ס�ABC����PEF�ס�PMN�ס�AMN�������������ʵ�y=S����MNFE=![]() ��EF+MN��OD=
��EF+MN��OD=![]() ����2x��6+x������4��
����2x��6+x������4��![]() x��=����x��4��2+4��������ֵ����.
x��=����x��4��2+4��������ֵ����.
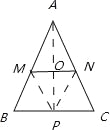
�⣺��1������AP����MN��O��
������AMN��MN���ڵ�ֱ���۵���ʹ��A�Ķ�Ӧ��ΪP��
��OA=OP��AP��MN��AN=PN��AM=PM��
��MN��BC��
���AMN�ס�ABC��AO��MN��
��![]() ��
��
��BC=6��
��MN=3��
����MN=3ʱ����Pǡ������BC�ϣ�
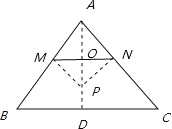
��2������A��AD��BC��D����MN��O��
��MN��BC��
��AO��MN��
���AMN�ס�ABC��
��![]() ��
��
��AB=AC=5��BC=6��AD��BC��
���ADB=90�㣬BD=![]() BC=3��
BC=3��
��AD=4��
��![]() ��
��
��AO=![]() x��
x��
��S��AMN=![]() MNAO=
MNAO=![]() x
x![]() x=
x=![]() x2��
x2��
��AO��![]() ADʱ��
ADʱ��
��������ã�S��PMN=S��AMN��
���MNP�������ABC�ص����ֵ����ΪS��AMN��
��y=![]() x2��
x2��
����AO=![]() ADʱ����MN=
ADʱ����MN=![]() BC=3ʱ��y��С����СֵΪ3��
BC=3ʱ��y��С����СֵΪ3��
��AO��![]() ADʱ��
ADʱ��
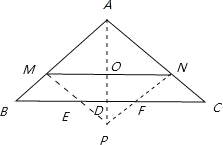
����AP��MN��O��
��AO��MN��
��MN��BC��
��AP��BC����AMN�ס�ABC����PEF�ס�PMN�ס�AMN��
��![]() ��
��![]() ��
��
����![]() ��
��![]() ��
��
��AO=![]() x��
x��
��![]() ��
��
��EF=2x��6��OD=AD��AO=4��![]() x��
x��
��y=S����MNFE=![]() ��EF+MN��OD=
��EF+MN��OD=![]() ����2x��6+x������4��
����2x��6+x������4��![]() x��=����x��4��2+4��
x��=����x��4��2+4��
����x=4ʱ��y�����ֵ�����ֵΪ4��
������������x=4ʱ��y��ֵ������ֵ��4��

����Ŀ��ijУ��չ����ͳ�Ļ���֪ʶ��������֪��У���꼶������Ů������ѧ��200�ˣ����и������ȡ20��ѧ�����г������飬���������֪ʶ�����ɼ�������100�֣����������������õ����沿����Ϣ��
������74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74
����76 87 93 65 78 94 89 68 95 54 89 87 89 89 77 94 86 87 92 91
�ɼ� | 50��x��59 | 60��x��69 | 70��x��79 | 80��x��89 | 90��x��100 |
���� | 0 | 1 | 10 | 1 | 8 |
�� | 1 | 2 | a | 8 | 6 |
ƽ��������λ�������������������ʾ��
�ɼ� | ƽ���� | ��λ�� | ���� | ���� |
���� | 84 | 77 | 74 | 145.4 |
�� | 84 | b | 89 | 115.6 |
����������Ϣ���ش��������⣺
��1��a���� ����b���� ����
��2������Ϊ���꼶ѧ���У���������Ů��������ɼ��Ϻã�Ϊʲô�������ٴ�������ͬ�ĽǶ�˵����
��3�����ڴ˴ξ����У���У���꼶ѧ����������ȡ��100�ֵĺóɼ�����ǡ����������������Ů�����ִ��������������ȡ���˲μ�����ľ�������������ǡ����һ��һŮ�ĸ��ʣ�