��Ŀ����
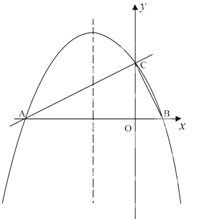
����Ŀ����ͼ����ƽ��ֱ������ϵxoy�У�ֱ��![]() ��x �ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����
��x �ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����![]() �Ҿ���A��C���㣬��x�����һ����Ϊ��B��
�Ҿ���A��C���㣬��x�����һ����Ϊ��B��
��1����ֱ��д����B�����ꣻ���������߽���ʽ��
��2������PΪֱ��AC�Ϸ����������ϵ�һ�㣬����PA��PC�����PAC����������ֵ���������ʱ��P�����꣮
��3�����������Ƿ���ڵ�M������M��MN��ֱx���ڵ�N��ʹ���Ե�A��M��NΪ��������������ABC���ƣ������ڣ�ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1����B��1,0����![]() ��2��4,P����2��3��;��3������M1��0��2��,M2����3,2��, M3��2����3��,M4��5����18��, ʹ���Ե� A��M��NΪ���������������ABC���ƣ�
��2��4,P����2��3��;��3������M1��0��2��,M2����3,2��, M3��2����3��,M4��5����18��, ʹ���Ե� A��M��NΪ���������������ABC���ƣ�
�������������������1���������ֱ��y=![]() x+2��x�ύ������꣬Ȼ�����������ߵĶԳ��Կ���õ�B�����ꣻ���������ߵĽ���ʽΪy=y=a��x+4����x��1����Ȼ��C��������뼴�����a��ֵ��
x+2��x�ύ������꣬Ȼ�����������ߵĶԳ��Կ���õ�B�����ꣻ���������ߵĽ���ʽΪy=y=a��x+4����x��1����Ȼ��C��������뼴�����a��ֵ��
��2�����P��Q�ĺ�����Ϊm���ֱ���õ�P��Q�������꣬�Ӷ��ɵõ��߶�PQ=-![]() m2��2m��Ȼ�����������ε������ʽ�����S��PAC=
m2��2m��Ȼ�����������ε������ʽ�����S��PAC=![]() ��PQ��4��Ȼ�������䷽���������PAC����������ֵ�Լ���ʱm��ֵ���Ӷ�����õ�P�����ꣻ
��PQ��4��Ȼ�������䷽���������PAC����������ֵ�Լ���ʱm��ֵ���Ӷ�����õ�P�����ꣻ
��3�����ȿ�֤����ABC�ס�ACO�ס�CBO��Ȼ������¼�������������ۼ��ɣ�����M����C���غϣ���M��0��2��ʱ����MAN�ס�BAC�������������ߵĶԳ��ԣ���M����3��2��ʱ����MAN�ס�ABC�� ������M�ڵ�������ʱ������ʱ����Ҫע�����������εĶ�Ӧ��ϵ��
�����������1����y=![]() x+2
x+2
��x=0ʱ��y=2����y=0ʱ��x=��4��
��C��0��2����A����4��0����
�������ߵĶԳ��Կ�֪����A���B����x=��![]() �Գƣ�
�Գƣ�
����B��������1��0����
�ڡ�������y=ax2+bx+c��A����4��0����B��1��0����
�����������߽���ʽΪy=a��x+4����x��1����
���������߹���C��0��2����
��2=��4a
��a=-![]()
��y=-![]() x2-
x2-![]() x+2��
x+2��
��2����P��m��-![]() m2-
m2-![]() m+2����
m+2����
����P��PQ��x�ύAC�ڵ�Q��
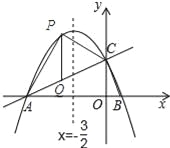
��Q��m��![]() m+2����
m+2����
��PQ=-![]() m2-
m2-![]() m+2����
m+2����![]() m+2��
m+2��
=-![]() m2��2m��
m2��2m��
��S��PAC=![]() ��PQ��4��
��PQ��4��
=2PQ=��m2��4m=����m+2��2+4��
����m=��2ʱ����PAC����������ֵ��4��
��ʱP����2��3����
��3����Rt��AOC��tan��CAO=![]() ��Rt��BOC��tan��BCO=
��Rt��BOC��tan��BCO=![]() ��
��
���CAO=��BCO��
�ߡ�BCO+��OBC=90����
���CAO+��OBC=90����
���ACB=90����
���ABC�ס�ACO�ס�CBO��
����ͼ��
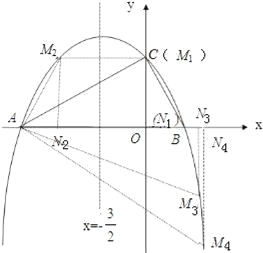
����M����C���غϣ���M��0��2��ʱ����MAN�ס�BAC��
�� ���������ߵĶԳ��ԣ���M����3��2��ʱ����MAN�ס�ABC��
�� ����M�ڵ�������ʱ����M��n��-![]() n2-
n2-![]() n+2������N��n��0��
n+2������N��n��0��
��MN=![]() n2+
n2+![]() n��2��AN=n+4
n��2��AN=n+4
��![]() ʱ��MN=
ʱ��MN=![]() AN����
AN����![]() n2+
n2+![]() n��2=
n��2=![]() ��n+4��
��n+4��
�����ã�n2+2n��8=0
��ã�n1=��4���ᣩ��n2=2
��M��2����3����
��![]() ʱ��MN=2AN����
ʱ��MN=2AN����![]() n2+
n2+![]() n��2=2��n+4����
n��2=2��n+4����
�����ã�n2��n��20=0
��ã�n1=��4���ᣩ��n2=5��
��M��5����18����
��������������M1��0��2����M2����3��2����M3��2����3����M4��5����18����ʹ���Ե�A��M��NΪ���������������ABC���ƣ�

 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�