题目内容
【题目】关于![]() 的方程
的方程![]() .
.
(1)求证:方程总有实根;(2)若方程的根为正整数,求整数![]() 的值.
的值.
【答案】(1)见解析;(2)m的值为0,±1.
【解析】
1)当m=1时,原方程为一元一次方程,通过解方程可得出m=1时方程有实数根;当m≠1时,由根的判别式△=4(m-1)2≥0,可得出m≠1时方程有实数根.综上即可证出结论;
(2)当m=1时,原方程为一元一次方程,通过解方程可得出m=1符合题意;当m≠1时,利用因式分解法解方程可得出方程的根,由方程的根为正整数结合m为整数即可得出m的值,综上此题得解.
解:(1)当![]() 即
即![]() 时,
时,![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]()
![]() ,
,
∴方程有根.
综上,不论m为何值,方程总有实根.
(2)当![]() ,
,![]() 符合题意
符合题意
当![]() 时,不妨设方程两根为
时,不妨设方程两根为![]() .
.
由题知![]()
又![]() 均为正整数
均为正整数
∴![]() 为正整数且
为正整数且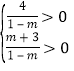
∴![]() ,2,4且
,2,4且![]()
∴![]()
综上m的值为0,±1.

练习册系列答案
相关题目