题目内容
【题目】将线段![]() 绕点
绕点![]() 逆时针旋转角度
逆时针旋转角度![]() 得到线段
得到线段![]() ,连接
,连接![]() 得
得![]() ,又将线段
,又将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
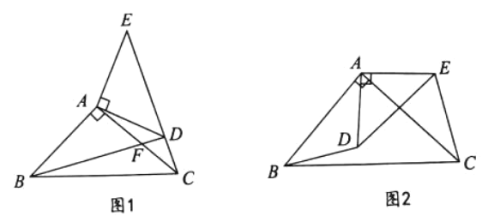
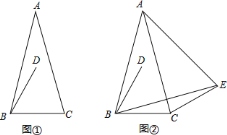
得线段![]() (如图①).
(如图①).
![]() 求
求![]() 的大小(结果用含
的大小(结果用含![]() 的式子表示);
的式子表示);
![]() 又将线段
又将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得线段
得线段![]() ,连接
,连接![]() (如图②)求
(如图②)求![]() ;
;
![]() 连接
连接![]() 、
、![]() ,试探究当
,试探究当![]() 为何值时,
为何值时,![]() .
.
【答案】![]()
![]() ;
;![]()
![]() ;
;![]() 当
当![]() 为
为![]() 时,
时,![]() .
.
【解析】
(1)由于线段AB绕点A逆时针旋转角度α(0°<α<60°)得到线段AC,根据旋转的性质得AB=AC,∠BAC=α,利用等腰三角形的性质和三角形内角和定理得到∠ABC=∠ACB=90°﹣![]() α,再由线段BC绕点B逆时针旋转60°得线段BD,根据旋转的性质得∠CBD=60°,然后利用∠ABD=∠ABC﹣∠CBD进行计算;
α,再由线段BC绕点B逆时针旋转60°得线段BD,根据旋转的性质得∠CBD=60°,然后利用∠ABD=∠ABC﹣∠CBD进行计算;
(2)由线段AB绕点B顺时针旋转60°得线段BE,根据旋转的性质得AB=AE,∠BAE=60°,则AC=AE,∠CAE=60°﹣α,利用等腰三角形的性质和三角形内角和得到∠ACE=∠AEC=60°+![]() α,然后利用∠BCE=∠ACB+∠ACE计算得到∠BCE=150°;
α,然后利用∠BCE=∠ACB+∠ACE计算得到∠BCE=150°;
(3)由线段BC绕点B逆时针旋转60°得线段BD,根据旋转的性质得BC=BD,∠CBD=60°,则可判断△BCD为等腰直角三角形,则∠BCD=60°,CD=BC,所以∠DCE=∠BCE﹣∠BCD=90°,加上∠DEC=45°,于是△DEC为等腰直角三角形,则CE=CD,所以CB=CE,然后利用“SSS”证明△ABC≌△AEC,得到∠BAC=∠EAC,所以α=![]() ∠BAE=30°.
∠BAE=30°.
(1)∵线段AB绕点A逆时针旋转角度α(0°<α<60°)得到线段AC,∴AB=AC,∠BAC=α,∴∠ABC=∠ACB,∴∠ABC=∠ACB=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α.
α.
∵线段BC绕点B逆时针旋转60°得线段BD,∴∠CBD=60°,∴∠ABD=∠ABC﹣∠CBD=90°﹣![]() α﹣60°=30°﹣
α﹣60°=30°﹣![]() α(0°<α<60°);
α(0°<α<60°);
(2)∵线段AB绕点B顺时针旋转60°得线段BE,∴AB=AE,∠BAE=60°,∴AC=AE,∠CAE=60°﹣α,∴∠ACE=∠AEC=![]() (180°﹣60°+α)=60°+
(180°﹣60°+α)=60°+![]() α,∴∠BCE=∠ACB+∠ACE=90°﹣
α,∴∠BCE=∠ACB+∠ACE=90°﹣![]() α+60°+
α+60°+![]() α=150°;
α=150°;
(3)如图②.
∵线段BC绕点B逆时针旋转60°得线段BD,∴BC=BD,∠CBD=60°,∴△BCD为等边三角形,∴∠BCD=60°,CD=BC,∴∠DCE=∠BCE﹣∠BCD=150°﹣60°=90°.
∵∠DEC=45°,∴△DEC为等腰直角三角形,∴CE=CD,∴CB=CE.
在△ABC和△AEC中,∵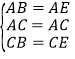 ,∴△ABC≌△AEC(SSS),∴∠BAC=∠EAC,∴∠BAC=
,∴△ABC≌△AEC(SSS),∴∠BAC=∠EAC,∴∠BAC=![]() ∠BAE=30°,即α=30°.
∠BAE=30°,即α=30°.
故当α为30°时,∠DEC=45°.

 名校课堂系列答案
名校课堂系列答案【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
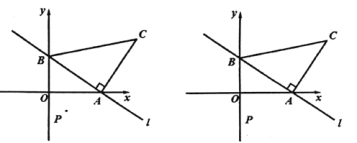
(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
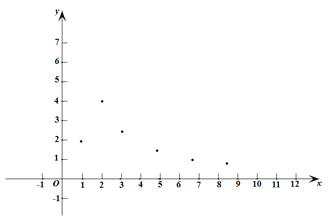
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为________;
②该函数的一条性质:__________________.