题目内容
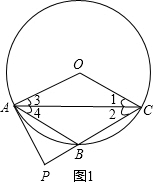
如图,A、B、C三点在⊙O上,
=
,∠1=∠2.
(1)判断OA与BC的位置关系,并说明理由;
(2)求证:四边形OABC是菱形;
(3)过A作⊙O的切线交CB的延长线于P,且OA=4,求△APB的周长.
 |
| AB |
 |
| BC |

(1)判断OA与BC的位置关系,并说明理由;
(2)求证:四边形OABC是菱形;
(3)过A作⊙O的切线交CB的延长线于P,且OA=4,求△APB的周长.
(1)OA∥BC.
理由:∵OA=OC,
∴∠1=∠3.
∵∠1=∠2,
∴∠2=∠3.
∴OA∥BC.
(2)证明:(方法一)∵
=
,
∴∠2=∠4.
∵∠2=∠1,
∴∠1=∠4.
∴AB∥OC.
由(1)得∴OA∥BC.
∴四边形OABC是平行四边形.
又∵OA=OC,
∴四边形OABC是菱形.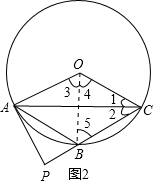
(方法二)∵
=
,
∴∠2=∠4.
由(1)得∠2=∠3,
∴∠3=∠4.
在△AOC与△ABC中,∠1=∠2,AC=AC,∠3=∠4,
∴△AOC≌△ABC.
∴OA=BA,OC=BC.
又∵OA=OC,
∴OA=AB=BC=OC.
∴四边形OABC是菱形.
(方法三)连接OB,
∵
=
,
∴∠3=∠4,AB=BC.
由(1)得OA∥BC,
∴∠3=∠5.
∴∠4=∠5.
∴BC=OC.
又∵OA=OC,
∴OA=AB=BC=OC.
∴四边形OABC是菱形.
(方法四)连接OB,∵
=
,
∴∠3=∠4.
又∵OA=OC,
∴OB垂直平分AC.
由(1)得OA∥BC.
∴∠3=∠5.
∴∠4=∠5.
∴BC=OC.
又∵∠1=∠2,
∴AC垂直平分OB.
∴AC与OB互相垂直平分,
∴四边形OABC是菱形.
(3)∵AP与⊙O相切,
∴∠OAP=90°.
由(1)得OA∥BC,
∴∠P=90°.
由(2)得OA=AB=4,
又∵OA=OB,
∴△OAB是等边三角形.
∴∠OAB=60°.
∴∠BAP=30°.
在Rt△ABP中,PB=
AB=2,AP=AB×cos∠PAB=4cos30°=2
.
∴△ABP的周长为4+2+2
=6+2
.
理由:∵OA=OC,
∴∠1=∠3.
∵∠1=∠2,
∴∠2=∠3.
∴OA∥BC.
(2)证明:(方法一)∵
 |
| AB |
 |
| BC |
∴∠2=∠4.
∵∠2=∠1,
∴∠1=∠4.
∴AB∥OC.
由(1)得∴OA∥BC.
∴四边形OABC是平行四边形.
又∵OA=OC,
∴四边形OABC是菱形.

(方法二)∵
 |
| AB |
 |
| BC |
∴∠2=∠4.
由(1)得∠2=∠3,
∴∠3=∠4.
在△AOC与△ABC中,∠1=∠2,AC=AC,∠3=∠4,
∴△AOC≌△ABC.
∴OA=BA,OC=BC.
又∵OA=OC,
∴OA=AB=BC=OC.
∴四边形OABC是菱形.
(方法三)连接OB,
∵
 |
| AB |
 |
| BC |
∴∠3=∠4,AB=BC.
由(1)得OA∥BC,
∴∠3=∠5.
∴∠4=∠5.
∴BC=OC.
又∵OA=OC,
∴OA=AB=BC=OC.
∴四边形OABC是菱形.
(方法四)连接OB,∵
 |
| AB |
 |
| BC |
∴∠3=∠4.
又∵OA=OC,
∴OB垂直平分AC.
由(1)得OA∥BC.
∴∠3=∠5.
∴∠4=∠5.
∴BC=OC.
又∵∠1=∠2,
∴AC垂直平分OB.
∴AC与OB互相垂直平分,
∴四边形OABC是菱形.
(3)∵AP与⊙O相切,
∴∠OAP=90°.
由(1)得OA∥BC,
∴∠P=90°.
由(2)得OA=AB=4,
又∵OA=OB,
∴△OAB是等边三角形.
∴∠OAB=60°.
∴∠BAP=30°.
在Rt△ABP中,PB=
| 1 |
| 2 |
| 3 |
∴△ABP的周长为4+2+2
| 3 |
| 3 |


练习册系列答案
相关题目









