��Ŀ����
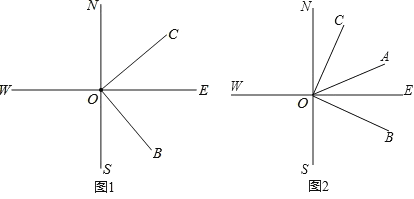
����Ŀ����ͼ1��ֱ��SN��ֱ��WE�ཻ�ڵ�O������ON��ʾ������������OE��ʾ����������֪����OB�ķ�������ƫ��m��������OC�ķ���Ϊ��ƫ��n������m���Ľ���n���Ľǻ�����
��1������m=60��д������OC�ķ���ֱ�ӻش���
����ֱ��д��ͼ���������BOE����ĽǼ����BOE�����Ľǣ�
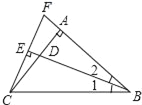
��2����ͼ2��������OA�ǡ�BON��ƽ���ߣ�
����m=70�����AOC�Ķ�����
����mΪ����Ƕȣ����AOC�Ķ�����������ú�m��ʽ�ӱ�ʾ��
���𰸡���1���ٱ�ƫ��30�㣻�����BOE����Ľ��С�BOS����COE�����BOE�����Ľ��С�BOW����COS����2����35�㣻�ڡ�AOC=![]() m�㣮
m�㣮
��������
��1����������ǵĶ������n��ֵ��Ȼ����ݷ���ǵĶ��弴�ɽ��
��������ǺͲ��ǵĶ��弴�ɽ��
��2�������������BON�Ķ�����Ȼ����ݽ�ƽ���ߵĶ��������AON��Ȼ�������AOC=��AON-��CON������⣻
���ⷨ������ͬ����70���ij�m����������⣮
��1���ٱ�ƫ��30�㣬
�⣺n=90�㩁60��=30����������OC�ķ����ǣ���ƫ��30��
�����BOE����Ľ��С�BOS����COE��
���BOE�����Ľ��С�BOW����COS��
��2����35�㣻
�⣺��BON=180�㩁70��=110�㣬
��OA�ǡ�BON��ƽ���ߣ�
���AON=![]() ��BON=55�㣬
��BON=55�㣬
�֡ߡ�CON=90�㩁70��=20�㣬
���AOC=��AON����CON=55�㩁20��=35�㣮
�ڡߡ�BOS+��BON=180�㣬
���BOS=180�㩁��BON=180�㩁m�㣮
��OA�ǡ�BON��ƽ���ߣ�
���AON=![]() ��BON=
��BON=![]() ��180�㩁m�㣩=90�㩁
��180�㩁m�㣩=90�㩁![]() m�㣮
m�㣮
�ߡ�BOS+��CON=m��+n��=90�㣬
���CON=90�㩁m�㣬
���AOC=��AON����CON=90�㩁![]() m�㩁��90�㩁m�㣩=90�㩁
m�㩁��90�㩁m�㣩=90�㩁![]() m�㩁90��+m��=
m�㩁90��+m��=![]() m�㣮
m�㣮

����Ŀ��ʢʢͬѧ��ij��У����ʱ�������˶������������еIJ�����Ϣ�����±�����
Ժϵ�������ɼ����� | |||
�������� | ʤ�� | ���� | ���� |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
ʢʢͬѧ���ѧϰ��֪ʶ������������⣬�����æ����������⣺
��1���ӱ��п��Կ�������һ����______��,ʤһ����_______����
��2��ij���ڱ���22����ǰ���£�ʤ���ܻ����ܵ����为���ܻ��ֵ�2������˵������.