题目内容
【题目】下图甲是任意一个直角三角形ABC,它的两条直角边的边长分别为a、b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.
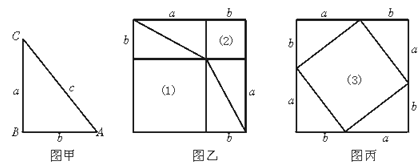
①图乙和图丙中(1)(2)(3)是否为正方形?为什么?
②图中(1)(2)(3)的面积分别是多少?
③图中(1)(2)的面积之和是多少?
④图中(1)(2)的面积之和与正方形(3)的面积有什么关系?为什么?
由此你能得到关于直角三角形三边长的关系吗?

【答案】见解析
【解析】
试题根据正方形的面积公式依次分析即可.
①图乙、图丙中(1)(2)(3)都是正方形.易得(1)是以a为边长的正方形,(2)是以b为边长的正方形,(3)的四条边长都是c,且每个角都是直角,所以(3)是以c为边长的正方形.
②图中(1)的面积为a2,(2)的面积为b2,(3)的面积为c2.
③图中(1)(2)面积之和为a2+b2.
④图中(1)(2)面积之和等于(3)的面积.
因为图乙、图丙都是以a+b为边长的正方形,它们面积相等,(1)(2)的面积之和与(3)的面积都等于(a+b)2减去四个Rt△ABC的面积.
由此可得:任意直角三角形两直角边的平方和等于斜边的平方,即勾股定理.

 智慧小复习系列答案
智慧小复习系列答案【题目】某中学在安全工作月中,进行了“防自然灾害﹣地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 40 | 120 | n | 4 |
频率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m的值为 , n的值为;
(2)根据表中的数据,请你计算“非常了解”的频率在如图中对应的扇形的圆心角的度数,并补全扇形统计图; 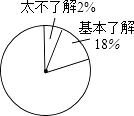
(3)若校一共有2400名学生,请根据调查结果估计全校学生中“比较了解”的人数为多少?
【题目】温度的度量有两种基本单位:摄氏温度(℃),华氏温度(℉).在温度计上,摄氏温度x与华氏温度y有如下表所示的对应关系:
x/℃ | … | -10 | 0 | 10 | 20 | … |
y/℉ | … | 14 | 32 | 50 | 68 | … |
按下列步骤确定y与x之间的函数关系式.
(1)在平面直角坐标系中描点、连线,画出图象;
(2)猜想能表示y与x之间关系的函数类型;
(3)确定y与x之间的函数关系式,并验证你的想法.