题目内容
【题目】学校实施新课程改革以来,学生的学习能力有了很大提高,陈老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(![]() :特别好,
:特别好,![]() :好,
:好,![]() :一般,
:一般,![]() :较差).并将调查结果绘制成以下两幅不完整的统计图,请根据统计图解答下列问题:
:较差).并将调查结果绘制成以下两幅不完整的统计图,请根据统计图解答下列问题:
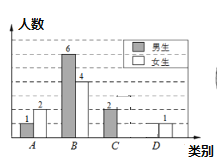
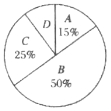
(1)本次调查中,陈老师一共调查了______名学生;
(2)将条形统计图补充完整;扇形统计图中![]() 类学生所对应的圆心角是_________度;
类学生所对应的圆心角是_________度;
(3)为了共同进步,陈老师从被调查的![]() 类和
类和![]() 类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
【答案】(1)20;(2)见解析,36;(3)见解析,![]()
【解析】
(1)由题意根据对应人数除以所占比值即可求出陈老师一共调查了多少名学生;
(2)根据题意补充条形统计图并![]() 类学生所对应的整个数据的比例乘以360°即可求值;
类学生所对应的整个数据的比例乘以360°即可求值;
(3)根据题意利用列表法或树状图法求概率即可.
解:(1)由题意可得:(6+4)÷50%=20;
(2)C类学生人数:20×25%=5(名),
C类女生人数:5-2=3(名),
D类学生占的百分比:1-15%-50%-25%=10%,
D类学生人数:20×10%=2(名),
D类男生人数:2-1=1(名),
补充条形统计图如图

![]() 类学生所对应的圆心角:
类学生所对应的圆心角:![]() ×360°=36°;
×360°=36°;
(3)由题意画树形图如下:
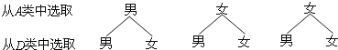
所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选两位同学恰好是一位男同学和一位女同学的结果共有3种.
所以P(所选两位同学恰好是一位男同学和一位女同学)=![]() =
=![]() ;
;
解法二:列表如下,A类学生中的两名女生分别记为A1和A2,
女A1 | 女A2 | 男A | |
男D | (女A1,男D) | (女A2,男D) | (男A,男D) |
女D | (女A1,女D) | (女A2,女D) | (男A,女D) |
共有6种等可能的结果,其中,一男一女的有3种,
所以所选两名学生中恰好是一名男生和一名女生的概率为![]() =
=![]() .
.

【题目】某数学兴趣小组根据学习函数的经验,对分段函数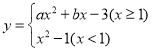 的图象与性质进行了探究,请补充完整以下的探究过程.
的图象与性质进行了探究,请补充完整以下的探究过程.
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 3 | 0 | -1 | 0 | 1 | 0 | -3 | … |
(1)填空:a= .b= .
(2)①根据上述表格数据补全函数图象;
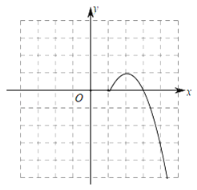
②该函数图象是轴对称图形还是中心对称图形?
(3)若直线![]() 与该函数图象有三个交点,求t的取值范围.
与该函数图象有三个交点,求t的取值范围.