题目内容
【题目】某数学兴趣小组根据学习函数的经验，对分段函数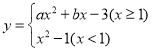
的图象与性质进行了探究，请补充完整以下的探究过程．
x | … | －2 | －1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 3 | 0 | －1 | 0 | 1 | 0 | －3 | … |
（1）填空：a＝ ．b＝ ．
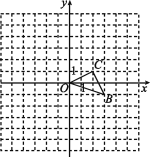
（2）①根据上述表格数据补全函数图象；
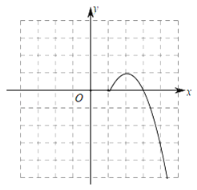
②该函数图象是轴对称图形还是中心对称图形？
（3）若直线
与该函数图象有三个交点，求t的取值范围．
【答案】（1）﹣1，4；（2）①见解析；②函数图象是中心对称图形；（3）
【解析】
（1）把（1，0），（2，1）代入y=ax2+bx-3构建方程组即可解决问题．
（2）利用描点法画出函数图象，根据中心对称的定义即可解决问题．
（3）求出直线y=
x+t与两个二次函数只有一个交点时t的值即可判断．
解：（1）把（1，0），（2，1）代入y＝ax2+bx﹣3
得
，解得
，
故答案为：﹣1，4．
（2）①描点连线画出函数图象，如图所示；
②该函数图象是中心对称图形．
（3）由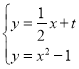
，消去y得到2x2﹣x﹣2﹣2t＝0，
当△＝0时，1+16+16t＝0，
，
由
消去y得到2x2﹣7x+2t+6＝0，
当△＝0时，49﹣16t﹣48＝0，
，
观察图象可知：当时，直线
与该函数图象有三个交点．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】若二次函数y=ax2+bx+c的x与y的部分对应值如下表：
| … | －4 | －3 | －2 | －1 | 0 | … |
| … | －5 | 0 | 3 | 4 | 3 | … |
（1）求此二次函数的表达式；
（2）画出此函数图象(不用列表).
（3）结合函数图象，当－4＜x≤1时,写出y的取值范围.
