题目内容
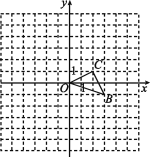
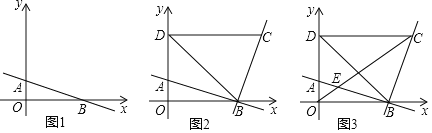
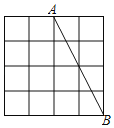
【题目】如图,正方形网格中,每个小正方形的边长均为1,线段AB的端点均在小正方形的顶点上,请按要求画出图形并计算.
(1)以线段AB为一腰的等腰△ABC,点C在小正方形的顶点上,且S△ABC=6;
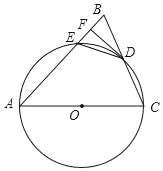
(2)以BC为对角线作平行四边形BDCE,点D,E均在小正方形的顶点上,且∠ABD=45°;
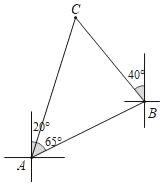
(3)连接DE,请直接写出线段DE的长.
【答案】(1)见解析;(2)见解析;(3)DE=2
【解析】
(1)利用数形结合的思想解决问题即可.
(2)利用数形结合的思想构造等腰直角三角形解决问题即可.
(3)根据D,E的位置求出线段DE的长即可.
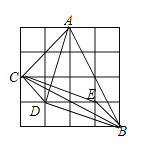
解:(1)如图,
![]()
∴△ABC即为所求.
(2)如图,
∵![]() ,
,
![]()
∴![]()
∴△ABD是等腰直角三角形,则∠ABD=45°
∴平行四边形BDCE即为所求.
(3)由图可知,DE=2.

练习册系列答案
相关题目