Question

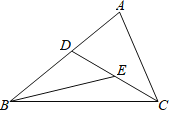
【题目】如图，△ABC中，D为边AB上一点，E是CD的中点，且∠ACD＝∠ABE．已知AC＝2，设AB＝x，AD＝y，则y与x满足的关系式为（　　）

A.xy＝4B.2xy﹣y2＝4C.xy﹣y2＝4D.x2+xy﹣2y2＝4

Answer 1

【答案】B

【解析】

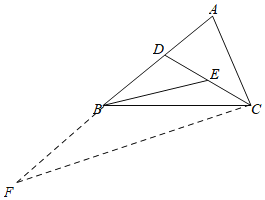
过C作CF∥EB交AB的延长线于F，利用相似三角形的性质求解即可．

过C作CF∥EB交AB的延长线于F，由于E为CD中点，故BF＝BD，∠F＝∠ABE，而∠ACD＝∠ABE，

∴∠ACD＝∠F，

∴在△AFC和△ACD中，

∠ACD＝∠F，∠A＝∠A，

∴△AFC∽△ACD，

∴＝，

∴AC2＝ADAF，

又∵BE∥CF，DE＝CE，

∴DB＝BF＝x﹣y，

∴22＝y（2x﹣y），

∴2xy﹣y2＝4，

故选：B．